Mahdi Abdeljaouad and Jeffrey A. Oaks
Abstract:
In 1305 al-Hawārī completed his commentary on Ibn al-Bannā’’s famous arithmetic book talkhīṣ aṯmāl al-ḥisāb. This is the only commentary, apart from Ibn al-Bannā’’s own, to have been written during the author’s lifetime. What distinguishes al-Hawārī’s book from the numerous later commentaries is its focus on numerical examples of the rules of calculation. We present here what we know about the author, his book, its salient features, and its influences.
Keywords:
al-Hawārī, Ibn al-Bannā’, Ibn Ghāzī, Şeker Zāde, arithmetic, double false position, algebra.
The famous mathematician and jurist Ibn al-Bannāʾ (1256-1321) wrote his talkhīṣ aṯmāl al-ḥisāb (Condensed [Book] on the Operations of Arithmetic) as a concise, easy to memorize introduction to the rules for calculating with Indian numerals on whole numbers, fractions, and roots, and for finding unknown numbers by double false position and algebra. The work was completed sometime before 1301 and became one of the most popular textbooks in Western Islam. It has been widely accessible
to scholars since it was edited and translated into French first by Aristide Marre in 1865, then again by Mohammad Souissi in 1969.[1] Popular and brief books naturally inspired commentaries. In fact, the first commentary of the talkhīṣ was written by Ibn al-Bannāʾ himself. In 701H/1301 he completed his Rafṯ al-ḥijāb ṯan wujūh aṯmāl al-ḥisāb (Removal of the Veil from the Face of the Workings of Arithmetic) in which he expanded the text of the Talkhīṣ by adding further explanations of the techniques, some numerical examples, and elements of number theory and combinatorics.[2] Among the many authors who composed commentaries of the Talkhīṣ after the death of the author are al-Ghurbī (2nd half 14th c.), al-Mawāhidī (ca. 1382), Ibn Zakariyyā (d. 1403-4), Ibn Qunfudh (d. 1407-8), al-ṯUqbānī (d. 1408), Ibn Haydūr (d. 1413), Ibn Majdī (d. 1447), al-Ḥabbāk (d. 1463), al-Qalaṣādī (d. 1486), and Muḥammad al-Ghazzī (16th c.). In the other direction, Ibn al-Hāʾim (d. ca. 1412) wrote an even more condensed version of the Talkhīṣ, and Ibn Marzūq (d. 1438), al-Wansharīsī (d. 1548-9), Ibn Ghāzī (d. 1513), and Ibn al-Qāďī (d. 1616) put the contents of the Talkhīṣ to verse.[3]
One person is known to have written a commentary of the Talkhīṣ while the author was still living. Al-Hawārī (fl. early 14th c.), one of Ibn al-Bannā’’s students, completed his al-Lubāb fī sharḥ Talkhīṣ aṯmāl al-ḥisāb (The Essential Commentary on Condensed [Book] on the Operations of Arithmetic) in 1305. We are currently preparing an edition, translation, and commentary of this book, and in this article we present what is known about the author, followed by salient features of the work and its later influences.
The author
Al-Hawārī’s full name is given in the manuscripts of his book as ṯAbd al-ṯAzīz ibn ṯAlī ibn Dāwud al-Hawārī al-Miṣrātī.[4] The kunya “al-Miṣrātī” refers to the tribe or the city of the Libyan Miṣrāta. Following Lamrabet and Cheddadi, this implies that al-Hawārī hailed from the Berber tribe named Hawārī which emigrated from Libya to Morocco before the ninth century.[5]
Al-Hawārī relates in his chapter on double false position that Ibn al-Bannāʾ dictated to him certain procedures “on Wednesday, the twenty-eighth of the month of Rajab in this year”. This can only be the year 704H, so the date corresponds to Gregorian February 24, 1305, and it places al-Hawārī in Marrakesh at the time. Less than four months later he finished writing his commentary. The Madina MS reports that it was completed on Saturday, 18 Dhū al-Qaṯda, 704H, which corresponds to Gregorian June 12, 1305.
Al-Hawārī is not known to have written any other books, and we know nothing more of his life or career.[6] Four modern sources give the date of his death as 744 or 745H, but we have not found any support for this in the manuscripts.[7]
The manuscripts
We consulted five manuscripts for our edition:
Madina, MS Ḥikmat 21 ḥisāb. 63 ff, 16 lines per page, 16 x 21 cm. This is followed by a short work of one page commencing “What was said about subtraction by seven”. The title is given in the explicit as: al-Lubāb fī sharḥ Talkhīṣ aṯmāl al-ḥisāb li Ibn al- Bannāʾ (“The Essence of Commentary on Condensed [Book] on the Operations of Arithmetic by Ibn al-Bannāʾ”)[8]. This manuscript is the oldest of the four. The copyist completed it on 18 Rabīʿ I, 746H (Gregorian July 19, 1345).
Istanbul, Süleymaniye Library, MS Şehit Ali Paşa 1977/2, ff. 54a- 103b. Copied 20 Ramaḍān 880H/11 January 1476 in Constantinople. This MS carries the title Sharḥ al-Talkhīṣ fī al-ḥisāb lī al-Hawārī (“Commentary on the Condensed [Book] on Arithmetic by al-Hawārī”). The copyist distinguished Ibn al-Bannāʾs text from al-Hawārī’s comments by placing in front of Ibn al-Bannāʾs extracts the letter “ص ” (ṣād), which stands for muṣannaf (original text),[9] while passages of al-Hawārī are preceded by the letter “ ش ” (shīn), which is the first letter of the word shārḥ (commentary). The London, India Office MS (see below) employs the “ص ” and “ش ” similarly.[10]
Oxford, MS Marsh 378/3, ff. 109a-162a. Dated 1444 according to Woepcke.[11] Here the title is Kitāb al-lubāb, wa huwa sharḥ al- Talkhīṣ li Ibn al-Bannāʾ fī ṯilm12 al-ḥisāb (“Essential Book, which is a Commentary on the Condensed [Book] of Ibn al-Bannāʾ on the Science of Arithmetic”).
Tunis, National Library of Tunis MS 9940. 32 ff., 22 x 26 cm, 29 lines per page. Copied 4 Jumādā II, 1082H/October 8, 1671 in Damascus. The title is given here merely as Kitāb sharḥ al-Talkhīṣ (“Book of Commentary on the Talkhīṣ”). In this manuscript Ibn al- Bannāʾs passages are preceded by the letter “م” (mīm), which stands for matn or muʾallaf, both of which mean “[original] text” and al- Hawārī’s comments start with a “ش” (shīn) for sharḥ (commentary).
Tehran, Library of Parliament MS 2672/2 ff. 10a-56b, copied before 972H/1564. The title page shows Kitāb al-lubāb fī sharḥ Talkhīṣ aṯmāl al-ḥisāb (“The Essence of Commentary on Condensed [Book] on the Operations of Arithmetic”).
Other known manuscripts, which we could not access, are: Madrid, Escorial MS 948/2, incomplete, copied 867H/1462 Madrid, Escorial MS 953/1, ff. 2b-79a, copied before 957H/1550 London, India Office MS 770/3 ff. 19b-69b copied 856H/1452 Rich (Morocco), Ḥamzāwiyya Library MS 145/2, 117 ff Tamegroute (Morocco), al-Khizāna al-Nāsiriya MS 3080
Rabat, Bibliothèque Générale MS Q846, 69 ff.
Rabat, Bibliothèque al-Ḥasaniyya MS 2186/2, 97 ff, incomplete and mixed up
Damascus, al-Ẓāhirīya Library MS 6666/1, ff. 1b-112b, copied 1002H/1594
Cairo, Central Library of Islamic Manuscripts of the ministry of
waqf, MS 1077, 80 ff. Copied 1270H/1853
Two manuscripts are reported to contain al-Hawārī’s commentary but do not: Istanbul, SM Laleli 2780 and Cairo, Falak 6829/1. ff. 1a-53b, copied 1050H. The second of these is probably Ibn Majdī’s commentary. The new digital catalogue of the Cairo Library confirms that MS 6829 is Hawārī’s sharḥ.
Comparing al-Hawārī’s al-Lubāb with his masters’ Talkhīṣ and Rafṯ al-ḥijāb
In Rafṯ al-ḥijāb Ibn al-Bannāʾ expounded on his Talkhīṣ with further explanations, linguistic justifications, as well as some numerical examples. By contrast, al-Hawārī wrote in his introduction that his main goal was to provide numerical examples lacking in both the Talkhīṣ and Rafṯ al-ḥijāb. In fact, the book contains very few elaborations on Ibn al-Bannāʾs rules. Al-Hawārī reproduces the entire text of the Talkhīṣ and places his numerical examples after each of Ibn al-Bannāʾs explanations.
We have found that 32 of the 284 numerical examples in al- Hawārī’s commentary are taken from Rafṯ al-ḥijāb. The following table gives the distribution by type of the number of these borrowed examples. Ibn al-Bannāʾs book is not mentioned in any of them:
| Whole numbers | Fractions | Roots | Scales | Algebra | Total | |
| al-Hawārī’s own | 96 | 32 | 54 | 6 | 64 | 252 |
| from Rafṯal-ḥijāb | 1 | 13 | 10 | 3 | 5 | 32 |
In addition, eight problems on summing numbers from al-Lubāb are also in Ibn al-Yāsamīn’s (d. 1204) Talqīḥ al-afkār fī’l-ṯilm bi- rushūm al-ghubār (“Grafting of opinions of the work on dust- figures”).[12] In an unrelated passage al-Hawārī quotes Ibn al- Yāsamīn, so of course he was familiar with that mathematician’s work. Most of these summation problems are standard examples that are found in every book that explains the rules, such as adding the consecutive numbers from one to ten, adding the consecutive cubes of one to ten, etc.
The numerical examples in al-Hawārī that are not in Rafṯ al-ḥijāb
are also not in any other known source, including Ibn al-Bannāʾs al-Maqālāt al-arbaṯ,[13] his algebra book al-Uṣūl wa’l-muqaddimāt fī’l- jabr wa’l-muqābala (henceforth Algebra),[14] or in the arithmetic books by al-Ḥaḍār, Ibn al-Yasamīn, or Ibn Munṯim.[15] It thus appears that these examples are al-Hawārī’s own. The vast majority of al-Hawārī’s problems are purely arithmetical. Very few of them are framed in the muṯāmalāt (business) style.
Al-Hawārī includes seven passages from Rafṯ al-ḥijāb that are indicated as coming from the Talkhīṣ, but which are not in Souissi’s edition.[16] It seems that in the course of dictating his Talkhīṣ Ibn al- Bannāʾ inserted material from his commentary. In three other places al-Hawārī mentions explanations given by Ibn al-Bannāʾ in which he cites Rafṯ al-ḥijāb explicitly.[17]
One passage in al-Hawārī’s book belongs to the Talkhīṣ but is absent in Souissi’s edition. In the section on summing number we
find “If the disparity of the numbers is a known number other than doubling, then multiply the disparity by the number of numbers less one. Adding the first number to the result gives the last number. Add it to the first, and multiply it by half of the number of numbers. It yields the required answer.”[18] This passage is also attributed to the Talkhīṣ in al-Qalaṣādī’s commentary.[19] This section on addition of numbers, including the added paragraph, is nearly identical word-for-word to the treatment in Ibn al-Yāsamīn’s Talqīḥ al-afkār. Ibn al-Bannāʾ seems to have copied it from this book .[20]
A little before this al-Hawārī ascribes the following passage to the Talkhīṣ “If the situation is different, then multiply the remainder by the first <square> to get the required number. A different situation is when the first square is not one.” The first sentence is in Ibn al-Yāsamīn’s Talqīḥ al-afkār, Souissi’s edition of the Talkhīṣ, and al-Qalaṣādī’s commentary, but the second sentence is not in any of them.
Still other passages in al-Lubāb attributed to the Talkhīṣ are not in Souissi’s edition, or in any other known text, including the commentaries by al-ṯUqbānī and al-Qalaṣādī. Here are the translations, with the location in Souissi’s edition of the Talkhīṣ where they would have gone:
“And by ‘power of ten’ (ṯaqd) we mean that the first <non- zero> digit is equal to a ten or a hundred or the like.” Place after [Souissi 1969, 50.10].[21]
“When looking for roots fractions come in four types. In one of them the numerator has a rational root and the denominator does too. Work it out as explained above. In the second type neither of them has a rational root, so work it out by the first rule. In the third type the denominator has a rational root but the numerator does not have a rational root. For this type one can work it out by the first rule or by the second. In the fourth type the numerator has a rational root and the denominator does not have a rational root, so work it out by the first rule”. Place after [Souissi 1969, 64.18]. The rules, with al-Hawārī’s numerical examples (omitted here), are also covered in [Ibn Ghāzī 1983, 155ff], but with no direct quotations.
“Another way to do this is to divide one of the numbers by the other. Then take the difference between the result and one, and then multiply by the divisor to get the required root. If the subtrahend or the minuend is more than one root or less, or if the ranks of their roots are different, then it is necessary to write them as one root or make them the same rank, like in addition.” Place after [Souissi 1969, 65.15]. Again, al-Hawārī includes numerical examples after each rule.
Symbols and notations in al-Hawārī’s book
Al-Hawārī’s book shows Indian (i.e. “Arabic”) notation for numbers, including fractions. The particle illā (“less”) is the only other symbol used in the notation. As is typical of Arabic books, the notation for numbers appears only in figures and not as part of the running text. Unlike most of the later commentaries of the Talkhīṣ, al-Hawārī does not use the Maghrebian algebraic notation.
Al-Hawārī explains the shapes of the nine figures by quoting a poem:
Someone has written a poem about them:
Alif and ḥāʾ then hajja followed by ṯuw
and after the ṯuw by an ṯayn. Draw
Hāʾ followed by an evident figure
looking like an anchor, and also you position two zeros for eight with an alif between them and wāw is the ninth <digit>; so understand it.[22]
This poem gives a mnemonic way to remember the Western forms of the digits. “Alif” stands for 1; ḥāʾ ح (
![]() ) for 2; ḥajja is the
) for 2; ḥajja is the
superposition of the letter ح over the letter ج ( ![]() ) for 3, ṯū عو (
) for 3, ṯū عو () for 4, ṯayn ع (
) for 5, a h?ʾ ه (
) for 6, and an anchor (
) for 7,
two zeros and an alif between them () for 8, and the letter wāw (
) for 9.[23] .
The writer of the Madina MS seems to have been an Eastern Arab who was not familiar with these forms, for he stricly follows the shapes described in the poem, below which he writes the Eastern forms (f. 4a):
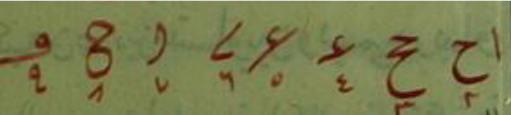
The Eastern forms are likewise written alongside the Western numerals for the next three folios, but after that only the Western forms are shown.
The Istanbul MS (f. 59a) shows the Western figures. Below is the number 9,367,184,225. In this one instance someone has written the Eastern forms above:

The Oxford MS shows the Eastern forms (f. 111b):

The Tunis MS (f. 3b) shows the Western forms with the poem, but reverts to the Eastern forms elsewhere:
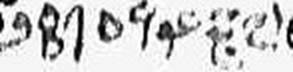
Numerals with the poem
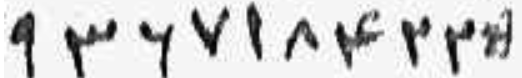
The number 9,367,184,225
The notations for fractions in al-Hawārī’s book originated before the twelfth century in Andalus or in the Maghreb. They are found in extant books written by al-Ḥaḍār, Ibn al-Yāsamīn, Ibn Munṯim and in Ibn al-Bannāʾs al-Maqālāt al-arbaṯ. Ibn al-Bannāʾ describes each type in the Talkhīṣ, but shows no examples. The following examples are given by al-Hawārī:
Simple (basāʾiṬ) fractions
and also and
.
Related (muntasib) fractions25
(in modern notation
. )
Distinct (mukhtalif ) fractions
(in modern notation
.)
Partitioned (mubaṯṯiď ) fractions
(in modern notation
.)
Like his professor Ibn al-Bannāʾ, the author of al-Lubāb considered finding the numerator of a fraction to be an important task. Most numerical examples on fractions are aimed at finding the numerator (basṬ). For example:
- The numerator of the simple fraction
is 7.
- The numerator of the related fraction
is 596.
- The numerator of the distinct fractions
is 122.
- The numerator of the partitioned fraction
is 105.
- The numerator of the diminished fraction of disconnected type
إلا
is 46. (in modern notation
).
Mixed fractions require explanation. If the integer is on the right,
like , it is added to the fraction. In modern notation this example is . If the integer is on the left, it is multiplied by
the fraction. Al-Hawārī’s
is to be read as
. When the integer is between two fractions it can be read three different ways. The example
might mean
,
, or
.
Operations on numbers
The algorithms presented by al-Hawārī are for use on a dust-board or other erasable surface. The layout of the numbers is the same as in the books of his predecessors. He typically writes the numbers in two parallel lines and the result above them as in these two examples:
To subtract 4968 from 5035, the work is shown as .
To multiply by
one writes
, with the result
.
Roots (Madina MS ff. 40b-50a).
Al-Hawārī’s treatment of roots is illustrated by not less than sixty numerical examples, most of them not known from prior works. In many instances he borrows passages from Rafṯ al-ḥijāb:
- the definition of rational and irrational numbers (Ibn al- Bannāʾ 1994, 283.3-7)
- the list of sufficient conditions for a number not to be a perfect square (pp. 284.14-285.1)
- conditions sufficient for a number to be a perfect square (pp. 285.2-6)
- applying the algorithm for computing the square root of 625 (pp. 284.4-9) and 729 (pp. 283.13-284.14).
- the arithmetical definition of binomials and apotomes (pp. 287.9-288.19), though the numerical examples are absent from Rafṯ al-ḥijāb.
Al-Hawārī’s work is similar to the chapter on roots in Ibn al- Bannāʾs Algebra but the numerical examples in the two books are different except for the calculations of the roots of the binomial and its apotome
.[24]
The method of scales (Madina MS ff. 50a-56a)
Double false position was called the “method of scales (kiffāt)” by many Arabic mathematicians because of the shape of the diagram used in working out the problems. Ibn al-Bannāʾ wrote in the Talkhīṣ “the method of scales is from the art of geometry”.[25] Randy Schwatrz wrote about the confusion that this statement has caused. Al-Qalaṣādī suggested that Ibn al-Bannāʾ linked double false position with geometry because of the drawing of the scales, and Franz Woepcke tried to read هندسة (geometry) as هند (Indian) to make the association instead with Indian numerals.[26] Al-Hawārī finally clarifies the statement: “It comes from the art of geometry because the ratio of the error of each scale to the difference between the scale and the unknown number is as the ratio of the assigned
number to the unknown.[27] -This comes from switching and separating. Switching the ratio of the <calculated> portion to its scale to the ratio of the assigned number to the unknown, as was made clear in Rafṯ al-ḥijāb.” There, in his own commentary, Ibn al- Bannāʾ wrote “the ratio of the error of each scale to the difference between the scale and the unknown number is as the ratio of the assigned number to the unknown”.[28] So by “geometry” Ibn al- Bannāʾ was referring to the geometric ratio of numbers. Later Ibn Ghāzī would write “The above shows that the scales are one of the two kinds of geometrical proportions”.[29]
After illustrating the method with five numerical examples, al- Hawārī writes that Ibn al-Bannāʾ dictated to him three more procedures used in the method of scales. These procedures are not found in Ibn al-Bannā’’s other known published works:[30]
Regarding this, my professor, the jurist and great erudite Abū al-‘Abbās <Ibn al-Bannāʾ>, God bless him, dictated to me while I was studying with him on Wednesday, the twenty-eighth of the month of Rajab in this year:[31]
There are three procedures. One of them is that you multiply the difference between the scales by one of the errors. If the two errors both exceed or both fall short, you divide the product by their difference. If one of them exceeds and the other falls short, you divide the product by their sum. If the selected error falls short, multiply the result of the division by the scale associated with the error. You add the result of this to the scale which you multiplied by its error if it falls short, and you subtract it from it if it exceeds. This gives the required <number>.
The second procedure is that you multiply the difference between the scales by the sum of the errors if they both exceed or both fall short, and you divide by their difference. If one of them exceeds and the other falls short, you multiply the difference between the scales by the difference between the errors, and you divide by the sum of the errors. Keep this result in mind. If you want, you can add this remembered number to the difference between the scales and take half the sum. You add it to the scale with the larger error if it falls short, and you subtract it from it if it exceeds, to get the required <number>.
And if you wanted, take the remembered number and the difference between the scales, and subtract the smaller from the larger, and take half of the remainder. Add it to the scale with the smaller error if it falls short, and subtract it from it if it exceeds, to get the required <number>.
The third way is that you multiply the difference between the scales by your assigned number. If the errors both exceed or both fall short, you divide the product by their difference, and if one of them exceeds and the other falls short, you divided the product by their sum, to get the required <number>. So know it.
While all of the problems solved by double false position in Ibn al-Bannā’’s Talkhīṣ are based on proportion, al-Hawārī adds two intricate problems and their solutions from Rafṯ al-ḥijāb in which “scales are used to find the unknown in cases without proportions”.[32] No figures are found in extant copies of Rafṯ al- ḥijāb, but in his al-Lubāb al-Hawārī adds one figure for each problem. Below are translations of the problems with al-Hawārī’s diagrams:[33]
Three men want to buy a horse. The first says to the second, give me half of what you have, and together with what I have, I will have the price of the horse. The second says to the third: give me a third of what you have, and together with what I have, I will have the price of the horse. And the third says to the first, give me a fourth of what you have, and together with what I have, I will have the price of the horse.
We choose one scale for the three men. We assign to the first man whatever we want, so we make it four. The second also has whatever we want, so we make it two. Then we calculate the price of the horse, which is five. We put it above the dome,[34] which is what we will confront. The third man has, by calculation, nine. So if we added a fourth of what the first has, it comes to ten. The error of the first scale with these three numbers is five, which exceeds.
Then we turn to the other scale. We fix four for the first man, the same as we chose for him in the first scale, and we make the second whatever we want. We see that it should not be eight or more, since it would leave the third with nothing. So know it. So we make it six. This makes the price of the horse, which we confront, seven. We put it above the dome also, and from this the third necessarily has three. Adding this to a fourth of what the first has gives four. The error of the second scale37 is then three, falling short. This is the figure:
So we multiply the error of each scale by what each one has in the other scale, and we divide the sum of the two products by the sum of the errors, as mentioned above, to get what each one of them has and the price of the horse. This gives us what the first has, which is the four, and the second four and a half, the third five and a fourth, and the price of the horse is six and a fourth.
From here, following Ibn al-Bannāʾ in Rafṯ al-ḥijāb, al-Hawārī discusses the way to adjust the answer if integers are required or if
the price of the horse is given. Also Ibn al-Bannāʾ solved this very problem by algebra in his Algebra.[35] Similar problems with algebraic solutions can be found in al-Karājʿ’s al-Fakhrī.[36]
The second problem is:[37]
Forty birds, among which are geese, chickens, and starlings,
<all> for forty dirhams. The starlings are eight for a dirham, the chickens are one for two dirhams, and the geese are one for three dirhams. How many were chosen of each kind of bird?
This type <of problem> may not have a solution. Two conditions must be satisfied. One is that the solution must consist of whole numbers, not fractions. Second, the price of the cheapest one, if multiplied by the number of birds, must be less than the total price; and the price of the most expensive bird multiplied likewise must be greater than the <total> price.
It is obvious in this problem that the number of starlings must be eight or sixteen or twenty-four or thirty-two, and no other number. If there were eight, then thirty-two birds remain, and thirty-nine remains of the cost. If we check the second condition, the product of the remaining birds by the price of the cheapest one is larger than the number of the price, which is not valid. If we make the starlings sixteen, and we again check the remaining price, we find that it is also not valid. If we make the starlings twenty-four, and we again check what remains, the two conditions are met.
So we suppose there are twenty-four starlings, and we assign the chickens whatever we want. Suppose they are eight. Then this leaves eight geese. The error in the price is three dirhams, which exceeds. Then we turn to the other scale. We suppose there are twenty-four starlings, the same as before, since it is a condition for this work that a number is repeated in the two scales. And we make the chickens whatever we want, but not <the same as> the first, so let it be fourteen. Then the number of geese is two. The error is three dirhams falling short. Here is the figure:
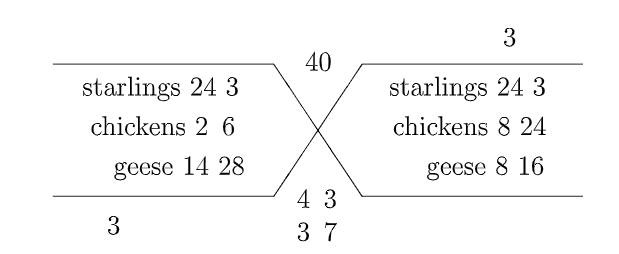
We work it out as before to get the required number. If we want we can first find the number of each type of bird, or the price of each type. The price of the starlings is three, and there are twenty- four of them. There are five geese and their price is fifteen, and there are eleven chickens and their price is twenty-two. If we suppose there are thirty-two starlings, it is not valid since the condition on the remaining <birds> is not met. Thus there is only one way to solve this problem.
Problems concerning the purchase of different kinds of birds date back at least to Abū Kāmil (d. 930), who solved them by algebra.[38]
We have found no earlier examples of indeterminate problems solved by scales. The only subsequent author we know to include them is Ibn Ghāzī in his Bughyat al-Ṭullāb fī sharḥ munyat al-ḥussāb (“Aim of the Students in Commentary on Desire of Reckoners”, 1483), but he writes that he took the problems from Rafṯ al-ḥijāb.[39]
A different use of muʿādala in algebra
The verb used to equate the two sides of an algebraic equation in medieval Arabic is ṯadala (“equal”), and the associated noun muʿādala is the word for “equation”.[40] Ibn al-Bannāʾ naturally uses both words with these meanings in his Talkhīṣ, but he also introduces a different meaning of muʿādala with language that is not at all clear. After briefly presenting the meanings of al-jabr (restoration) and al-muqābala (confrontation), he writes “And muʿādala is that you restore the deleted to the appended, and you subtract the appended from the appended and the deleted from the deleted of things of the same kind.”[41] His explanation of this passage in Rafṯ al-ḥijāb does little to help: “And restoring the deleted to the appended is al-muʿādala with restoration, and subtracting the appended from the appended and the deleted from the deleted of things of the same kind is al-muʿādala with confrontation.”[42] At least here he indicates that somehow one performs “al-muʿādala with restoration” and “al-muʿādala with confrontation”. Al-Qalaṣādī, in his commentary, does not explain muʿādala at all. He only describes the simplification of equations with al-jabr and al-muqābala.[43]
Al-Hawārī and al-ṯUqbānī clear up the confusion in their commentaries. Their specific examples are worth reviewing because there may be a link between this new meaning of muʿādala and the phrase ugagliare le parti (equalize the parts) in medieval Italian algebra. Al-Hawārī gives two examples. He does it not in the context of equations, but for the subtraction of one algebraic expression form another in which one of them has a deleted term (in an expression like “a māl less three things” (
) the “māl” is a diminished quantity from which “three things” have been deleted47). Subtraction problems are like equations in that any amount added to or subtracted from one part must also be done to the other part.
The first example is to “subtract two and a thing (
) from a māl less three things (
)”. He transforms the problem into an equivalent subtraction by restoring (al-jabr) the diminished māl, which amounts to making the
a full
, and by “balancing” or “equalizing” (muʿādala) the problem by adding
to the other part:
We begin with the things in the diminished minuend, which is three. We add it to the two parts at once. This is what is meant by equalization (al-muʿādala) with restoration (al-jabr), since we add to the māl what it is associated with, which is three things. Thus we restore <the māl> by addition, which removes the deletion. It becomes larger, as we want for the minuend. Then we equalize (nuṯādilu, from the verb ṯādala for muʿādala), by which we restore the subtrahend by the amount we added in the minuend, which is by the three things. This works because subtracting two numbers gives the same result as subtracting them after we added a number to both of them, or after subtracting a number from both of them. Once this is done, the problem becomes: If someone said “subtract two and four things from a māl ”. Then work it out as before. The remainder is the required number, which is a māl less four things and less two. So know it.
The second problem is to “subtract fifty-two dirhams less five things (
) from two cubes and thirty dirhams (
)”. Here al-Hawārī first does a “restoration with equalization”, followed by a “confrontation with equalization”:
We begin with the things in the diminished subtrahend, which are five. We add it to the two sides at once, as before. The problem becomes: if someone said, subtract fifty-two dirhams from two cubes and five things and thirty dirhams.
Now consider the dirhams on the two sides. We take away the smaller quantity from the two sides at once. The problem reduces to: if someone said, “subtract twenty-two dirhams from two cubes and five things”. This is confrontation (al-muqābala) with equalization (al-muʿādala), since we took thirty away from the subtrahend. It becomes smaller than the original subtrahend. So we equalize, by which we take from the minuend the same amount we subtracted from the subtrahend. Work it out as before. We work it out with the remainder as before. So remove what remains. This is the required amount, which is two cubes and five things less twenty-two dirhams.
Today we perform a subtraction like
by distributing the minus sign and combining like terms. But in medieval algebra there was no equivalent of “distributing the minus sign”. The
was regarded as a deficient or diminished 52, so the rule for subtracting it required some explanation. Al-Khwārizmī gave proofs with geometric diagrams to justify the results of adding or subtracting diminished quantities, while most later algebraists, al- Hawārī included, worked them by “restoring” the diminished term(s) and adding the same amounts to the other side. We have not seen the “confrontation” (al-muqābala) of like terms in subtractions like this in other books.
In his commentary on the Talkhīṣ al-ṯUqbānī illustrates this meaning of muʿādala in the context of equations. He simplifies the
equation
by removing the exceptions “less two things” and “less three” (the restoration), and adding the
to
and adding the 3 to 10 (the equalization) to get
:
And if you wanted to remove the troublesome exceptions from the two sides, then take them away from them, and add to each side what had been deleted from the other side. So you add two things to the five things and three to the ten. So your equation becomes: thirteen equal seven things. All of this is called restoration (jabara), which is what is meant by saying al-jabr and al-muʿādala, though the term al-jabr wa’l-muqābala (restoration and confrontation) is on the whole the generally accepted phrase for this manipulation of both parts. This term became the way to name the entire process, or to <name> the process without the long explanation <required by> the other term.[44]
Al-ṯUqbānī then illustrates Ibn al-Bannāʾs statement “you subtract the appended from the appended and the deleted from the deleted of things of the same kind” by simplifying
to
. Although al-ṯUqbānī does not say so explicitly, Ibn al- Bannāʾ called this “equalization with confrontation” in Rafṯ al- ḥijāb.
We now have a clearer understanding of Ibn al-Bannāʾs meaning of muʿādala (equalization). In “restoration with equalization” the restoration (al-jabr) of a diminished quantity only affects that quantity. To equalize or balance (al-muʿādala) the problem or equation, one must also add the same amount to the other side. One applies “confrontation with equalization” when there are like terms in the two parts. The confrontation is the subtraction of the smaller term from the larger, and the equalization is the removal the smaller from the other side. Equalization, then, is the compensating operation to balance the problem or equation after restoring or confronting.
Curiously, Ibn al-Bannāʾ does not use muʿādala for this purpose in his Algebra. In fact, we have not found the word used this way outside these two commentaries. It may have been invented by Ibn al-Bannāʾ while he wrote the Talkhīṣ to emphasize to students the need for operating on both sides of an equation or subtraction. Whatever its origin, it never came into common use.
Al-ṯUqbānī’s remark that al-jabr wa’l-muqābala is “the generally accepted phrase” for restoring/confronting and equalizing is born out in many Arabic books.[45] Al-Hawārī, for example, uses the phrase al-jabr wa’l-muqābala this way: “a māl less three things equal twenty-four dirhams less five things (
). So you restore and confront (tajbir wa tuqābil) as before, and the problem becomes: a māl and two things equal twenty-four dirhams”.[46]
In place of the phrase al-jabr wa’l-muqābala most medieval Italian algebraists wrote either ristora le parti (restore the parts) or ugagliare le parti (equalize the parts). The earliest known use of the latter phrase is in Maestro Dardi’s 1344 Aliabraa Argibra. In problem 44, for example, he arrives at the equation
and writes “Now equalize the parts (raghuaglia le parte): subtract 25 numbers from each part, and you will have that
will be equal to the other part, which is 75 numbers.[47] The meanings of the words ristorare and uguagliare in Italian algebra are modified from the Arabic. Now “restoration” (ristorare, from the Arabic al-jabr) no longer serves to restore a diminished quantity, and “equalization” (uguagliare, from muʿādala) is no longer the compensating operation. Both now take the meaning of the Arabic phrase al-jabr wa’l-muqābala. We do not know if the Italian uguagliare descends directly from Ibn al-Bannāʾs muʿādala, but both terms refer to a “balancing” or “equalization” of the two
sides when simplifying an equation or subtraction.
Three problems dictated to al-Hawārī by Ibn al-Bannāʾ
Al-Hawārī concludes his book by presenting three recreational problems in arithmetic that were dictated to him by Ibn al-Bannāʾ. In each problem a person is asked to think of a secret number and to perform a succession of operations. At some point the person is asked to announce the value of the number resulting from the operations, from which the hidden number can be recovered.
Similar problems are found in other arithmetic books. Seven problems of this type are in Ibn al-Yāsamīn’s Talqīḥ al-afkār, three problems are in the last chapter of al-Maṯūna by Ibn al-Hāʾim (1389), and fourteen such problems are in Ibn Haydūr’s commentary of the Talkhīṣ (ca. 1400). Yaṯqūb al-Kindī (d. ca. 873) wrote a book on hidden numbers, the Risālā fī istikhrāj al-aṯdād al- muďmara (Treatise on Finding Hidden Numbers)[48]. We have not examined it so we do not know if his problems are of the same sort that are found in the later arithmetic books.
The problems posed in the books of Ibn al-Yāsamīn, Ibn al- Hāʾim, and Ibn Haydūr are different from the problems related to al-Hawārī by Ibn al-Bannāʾ.[49] Because they have not been published before, we include a translation here:
We conclude this work with three problems of witty reckoning. I do this following other arithmeticians, who continue to write similar problems at the end of their compositions.
One of them is that we tell someone to subtract his <secret> number from ten, then to subtract the square of the remainder from the square of his number.
If the <square of the> remainder is smaller, <we subtract it from the square of the secret number and> we ask for the remainder. We divide it by ten, and we add to the result half of its remainder from ten to get the secret number.
And if the square of the remainder is larger, we subtract the square of the secret number from it, and we ask for the remainder. We divide it by the ten, and we subtract the result from ten. Half the remainder is the secret number.
We can also ask the person to subtract his secret number from something other than ten. Working it all out still gives the required number.
The second problem. We tell someone to partition ten into two parts secretly. Then we tell him to divide the square of one of them by their surface [i.e. product], and we ask for the outcome. If we knew this, it is the ratio of one of the two parts to the other. So we partition the ten according to this ratio.
And similarly we can work with any number other than ten and partition it into two secret parts and we get them similarly.
The third problem. A secret number is partitioned into two secret numbers. How much is it? And how much are the two parts?
We tell him to multiply one of the parts by the other, square each one of them, then subtract the square of the smaller from the surface. Then we ask for the remainder. And he then subtracts the surface from the square of the larger, and we ask for the remainder. We then take the root of the difference between the two asked numbers, which is the difference between the parts. Then we divide the sum of the asked numbers by it to get the secret number, which is the sum of the two parts. If we add to it the root of the difference between them, it gives double the larger of them, and if we subtract it from their sum, it leaves double the smaller of them. So know it.
These three problems were dictated to me by my professor, the great jurist Abū al-ṯAbbās <Ibn al-Bannāʾ>, may God be pleased with him.
Modern mathematical explanation of the first problem:
We let x be the hidden number. If
, then set
. This number is announced (given). Divide y by 10
then add to the result half of 10 less the result, i.e. calculate . This is the secret number x.
If
, then set
. This number is announced (given). Then the secret number
.
Second problem
. Ask for
. This number is announced (given), and is the ratio . The solution can be obtained since we know that
and is given.
Third problem
, where
and all are hidden numbers.
Calculate
and announce the result, thus a is given.
Calculate
and announce the result, thus b is given.
Then![]() are now given.
are now given.
Then ![]()
Al-Hawārī’s influence
Two biographers working in the extreme Maghreb (modern Morocco) include notices about Ibn al-Bannāʾ, his Talkhīṣ, and
different commentators. Aḥmad ibn Muḥammad Ibn al-Qāďī (d. 1616) and Aḥmad Bābā al-Tunbuktī (d. 1627) each name five commentators, but not al-Hawārī. Further, the modern historian Muḥammad Ḥājjī has no entry for al-Hawārī in his Mawsūṯat aṯlām al-Maghrib, a ten volume chronological list of well-known North African jurists and scholars. Ḥājjī compiled his list from the biographical works of Ibn Qunfudh (d. 1508), al-Wansharīsī (d. 1512), al-Shanshāwunī (d. 1578), and others.[50] The lack of any biographical information on al-Hawārī suggests that he never held any official post, and his book leaves little doubt that he himself was not a first-rank mathematician. He was apparently merely a student of Ibn al-Bannāʾ who was authorized by his master to complete the Talkhīṣ with his own book on arithmetic.
Despite al-Hawārī’s lack of fame, al-Lubāb found its niche in mathematics education. Scrutiny of catalogues of libraries shows that copies of it were regularly made in the succeeding centuries and in different Islamic countries. In particular, al-Lubāb was used by some scholars in Istanbul. One of the extant manuscripts was copied there in 1476, and the only premodern biographer to mention al-Hawārī is the Ottoman historian Ḥājjī Khalīfa (d. 1657).[51] He makes a note of Ibn al-Bannāʾs Talkhīṣ, and the only commentary he mentions is al-Lubāb.
Apart from the extant manuscripts and the entry in Ḥājjī Khalīfa we have found three instances of al-Hawārī’s influence on the teaching of mathematics: (1) the borrowings from al-Lubāb made by Ibn Ghāzī in extreme Maghreb in 1483, (2) the collection of problems borrowed directly from al-Lubāb in mid-eighteenth century Istanbul by the Ottoman mathematician Şeker Zāde, and (3) the inclusion of al-Lubāb in the curriculum of the Tunisian al- Zaytūna mosque-university in 1875.
Al-Hawārī and Ibn Ghāzī
Muḥammad Ibn Ghāzī al-ṯUthmānī al-Miknāsī (1437-1513) condensed the Talkhīṣ into a poem of 461 verses titled Munyat al- ḥussāb (“Desire of Reckoners”). Later, in 890H/1483, he wrote a commentary on his poem titled Bughyat al-Ṭullāb fī sharḥ munyat al-ḥussāb (“Aim of the Students in Commentary on Desire of Reckoners”). In addition to quoting Ibn al-Bannāʾs Talkhīṣ and Rafṯ al-ḥijāb, Ibn Ghāzī also cites many other mathematicians, including al-Ḥaḍār, Ibn al-Yāsamīn, Ibn Qunfudh, and Ibn Haydūr. In two places Ibn Ghāzī cites al-Miṣrātī (i.e. al-Hawārī):
“… this <definition> has been explained in al-Maqālāt,[52] and this explanation is well-known; al-Miṣrātī and others based <their work> on it”. (Ibn Ghāzī 1983, 19.10-11)
“When referring to this in Rafṯ al-ḥijāb, Abū Muḥammad ṯAbd al-ṯAzīz al-Miṣrātī said, …” (Ibn Ghāzī 1983, 210.3)
Ibn Ghāzī also includes a great number of paragraphs and examples from al-Lubāb. But while he credits his borrowings from other mathematicians, he never cites his source when it is al- Hawārī’s book. Below is a list of the numbers of problems of different types taken by Ibn Ghāzī from al-Hawārī’s book that are not in Rafṯ al-ḥijāb:
- Sum of numbers : 16
- Casting out nines or sevens : 3
- Types of multiplications : 4
- Computing the numerator of a fraction : 11
- Operations on fractions : 10
- Operations on roots : 26
- Double false position (scales) : 6
- Algebra : 27
Additionally, there are two places where Ibn Ghāzī quotes Ibn al- Yāsamīn and Ibn Ṭāhir, and both quotations are also in al-Hawārī. It is likely that Ibn Ghāzī took them from al-Lubāb.[53]
Al-Hawārī and Şeker Zāde58 (d. 1787)
The second book we found to made use of al-Lubāb is Amthilatun min Talkhīṣ Ibn al-Bannāʾ wa al-Ḥāwī li Ibn al-Hāʾim (“Examples from Ibn al-Bannāʾs Talkhīṣ and al-Ḥāwī59 of Ibn al-Hāʾim”). It was compiled in the mid-eighteenth century by al-Sayyīd Faydh Allah Sarmid, known as Şeker Zāde. Şeker’s father, Muḥammad ibn ṯAbd al-Raḥmān al-Istanbūlī, was a renowned Ottoman calligrapher who taught him the Arabic language and the art of Arabic calligraphy. After a normal schooling in the Ottoman madrasas, Şeker Zāde was one of the best private students in mathematics and astronomy of Muṣṭafā ʿIdkī (d. 1769) and became specialized in these matters. Of his later career we know that in 1775 he was teaching mathematics and calligraphy as a mullah in the madrasa at Izmīr, and that he died in 1787.
While still a student Şeker Zāde made copies of many mathematics books by well-known authors such as Ibn al-Hāʾim, al- Qalaṣādī, and Ibn al-Bannāʾ. He also wrote his own books on the mathematics he had learned, including a sexagesimal multiplication table and an introduction to logarithms.[54] His Amthilatun falls into this latter category. The unique manuscript is an exercise book containing a collection of numerical examples illustrating the definitions and computational rules primarily from Ibn al-Bannāʾs Talkhīṣ, with some also from its derivative, Ibn al-Hāʾim’s al- Ḥāwī.[55] Well over a hundred problems from al-Lubāb are included
in Şeker Zāde’s Amthilatun, along with a scattering of problems taken from other books and some of the author’s own invention.
Traditional Arabic arithmetic books explain rules and concepts rhetorically. Notation is only presented here and there to illustrate what one would write out when actually doing the calculations. Şeker Zāde’s Amthilatun is remarkable in that it consists mainly of solutions to problems written entirely in notation. This is the same notation invented in the thirteenth century and popularized by al- Qalaṣādī and Ibn Ghāzī in the fifteenth century, including the notation for algebra that is absent in al-Hawārī. At the top of a typical section Şeker puts the title from the Talkhīṣ on the right and the similar one from al-Ḥāwī on the left, both written in red. Below this he puts the worked out examples in several vertical diagrams
For instance, when presenting the addition of numbers Ibn al- Bannāʾ writes a long paragraph detailing the steps of the addition scheme.[56] This paragraph is quoted by al-Hawārī63 and is illustrated by two numerical examples. In the first example, concerning the addition of 4043 and 2685, the scheme starts from the units digit, while in the second example concerning the addition of 978 and 456, the scheme starts from the last digit (i.e. the highest power). All of al-Hawārī’s explanations are rhetorical. In the excerpt shown below Şeker Zāde writes the title of the section On adding numbers with no known relation and under it he presents four problems taken from three different commentaries of the Talkhīṣ. The first two are the examples from al-Lubāb, the third is from Ibn Majdī’s Ḥāwī al- Lubāb and the last is from Ibn Haydūr’s al-Tamḥīṣ. Şeker Zāde indicates his source by writing “from al-Lubāb”, “from Ibn Majdī” and “from al-Tamḥīṣ” next to the examples
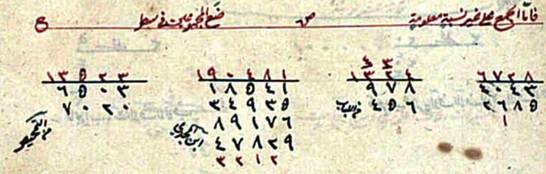
Occasionally Şeker Zāde will give a rhetorical rule or proposition taken either from the Talkhīṣ or from some other work on arithmetic or algebra. Here, too, each extract is attributed to the book from which it was borrowed by an expression such as “from the Talkhīṣ”, “from al-Lubāb”, etc. Borrowed extracts and given numbers are usually written in black, and the results of operations are in red. The systematic alternate use of red and black inks makes the pages quite visually appealing.
The total numbers of example problems from different sources are given in the following list:
111 from al-Hawārī’s al-Lubāb
Tuhfat al-Ṭullāb by Ibn Haydūr al-Tādilī (d. 1413),
7 from Sharʿ Talkhīṣ ṯamāl al-ʿiṣāb lī Ibn al-Bannāʾ by Qalaḍādī (d. 1486),
7 from al-Qawl al-mubdiṯ fī sharʿ al-muqniṯ by Sibṭ al-Māridīnī (d. 1506),
6 from Ḥāwī al-lubāb fī sharʿ al-Talkhīṣ by Ibn Majdī (1447),
16 from ten other authors.
Şeker also borrows (folio 27a) the same citation from Ibn al- Yāsamīn as Ibn Ghāzī, but he explicitly attributes it to al-Lubāb:[57]

The Zaytūna reform
Among the 217 courses taught in 1871 at the Zaytūna mosque university in Tunis, only five were reserved for mathematics, and these were merely rhymed poems and their commentaries on arithmetic and farāʾiď (inheritance). In 1875 the Tunisian Prime Minister Khayreddine announced a new curriculum for the Zaytūna mosque structured into three cycles: lower, intermediate, and superior, to be composed of 28 disciplines with recommended textbooks for each.
Ten works were prescribed for mathematics: two for the lower cycle and four each for the intermediate and superior cycles. The superior cycle included a text on Euclidean geometry, a commentary of a work on astronomy, and two arithmetic books: Ibn Ghāzī’s Aim of the students that we saw borrowed much from al-Hawārī, and al-Hawārī’s al-Lubāb. It was the first time that this book appeared in the list of recommended textbooks.
This new curriculum was an attempt to impose some government control over the institution and to inject some professionalism among the faculty. Even so, the selection of books was highly traditional and outdated. Nevertheless the ẓulamāʾ running the mosque severely criticized it and hindered its implementation. It is likely that the new curriculum was never fully implemented, and that mathematics instruction continued to be based on rote learning of urjūzas (poems), and on commentaries of the linguistic and stylistic aspects of their wording, thus preventing any effective practice of mathematics.
Conclusion
Despite the obscurity of its author, al-Lubāb remained a popular textbook in the centuries after it was composed, making its way to Istanbul and into the curriculum of nineteenth century Tunisia.
In writing al-Lubāb al-Hawārī set out to explain with numerical examples all the rules expressed in Ibn al-Bannāʾs Talkhīṣ. He of course intended his book for Arabic speaking arithmetic students, but he has also succeeded in helping us better understand Ibn al- Bannāʾs book and medieval Arabic arithmetic in general. Al- Hawārī’s book should be valuable today not just for historians, but also for mathematics educators as valuable testimony to the teaching of mathematics in fourteenth century North Africa.
Sources
Aballāgh, Muḥammad and Ahmed Djebbar, 2001. Ḥayāt wa muʾallafāt Ibn al-Bannāʾ (maṯa nuṣūṣ ghayr manshūra) [“Ibn al- Bannāʾs Life and Works (with unpublished texts”)]. Rabat: Publications de la Faculté des Lettres et des Sciences Humaines.
Abdeljaouad, Mahdi, 2011. “Şeker-Zāde (m. 1787) : Un témoignage tardif d’utilization des symboles mathématiques maghrébins inventés au 12e siècle”. Pp. 7-32 in: Actes du 10ème Colloque Maghrébin sur l'Histoire des Mathématiques Arabes (Tunis, 29-30-31 mai 2010). Tunis: L'Association Tunisienne des Sciences Mathématiques.
Bābānī, Ismāṯīl Bāshā, 1951-1955. Hadīyat al-ṯārifīn : asmāʾ al- muʾallifīn wa-athār al-muṣannifīn. 2 vols. Istānbūl: Wikālat al- Maṯārif.
Ben Cheneb, Mohammed, 1920. “Liste des abréviations employées par les auteurs arabes”. Revue Africaine 61, 134-138.
Maestro Dardi, 2001. Aliabraa Argibra: Dal manoscritto I.VII.17 della Biblioteca Comunale di Siena, ed. Raffaella Franci. Siena: Servizio Editoriale dell'Università di Siena.
Djebbar, Ahmed, 2002. “La circulation des mathématiques entre l’Orient et l’Occident musulmans”. Pp. 213-235 in: Yvonne Dold- Samplonius, Joseph W. Dauben, Menso Folkerts, and Benno van Dalen, eds. From China to Paris: 2000 Years Transmission of Mathematical Ideas. Stuttgart: Franz Steiner Verlag.
Djebbar, Ahmed, 2004. “Du nombre pensé à la pensée du nombre: quelques aspects de la pratique arithmétique arabe et de ses prolongements en Andalus et au Maghreb”. Pp. 303-322 in: C. Alvarez, J. Dhombres, and J.-C. Pont (eds), Actes de la « Rencontre Internationale de Peiresc sur la Pensée Numérique » (Peiresc, 7-10 septembre 1999). Bruxelles: Brepols.
Djebbar, Ahmed, 2007. “Du ludique au sérieux : l'exemple de l'arithmétique des IXe-XVe siècles”. Les Nouvelles d'Archimède 46, 22-23.
Ḥājjī Khalīfa, 2000. Kashf al-?unūn ṯan asāmī al-kutub wa-al- funūn, ed. Gustav Flügel. Bayrūt: Dar Sader. (originally published 1835-38)
Ḥājjī, Muḥammad, 1996. Mawsūṯat aṯlām al-Maghrib. Bayrūt: Dār al-Gharb al-Islāmī.
Harbili, Anissa, 1997. L’Enseignement des Mathématiques à Tlemcen au XIVe siècle à travers le Commentaire d’al-ṯUqbānī (m. 811/1408). Master Thesis, École normale supérieure Alger-Kooba.
Ibn al-Bannāʾ, 1969. Talkhīṣ aṯmāl al-ḥisāb. Texte établi, annoté et traduit par Mohamed Souissi. Tunis: Université de Tunis.
Ibn al-Bannāʾ, 1984. Māqālat fī’l-ḥisāb, ed. A. S. Saidan. ṯAmmān: Dār al-Furqān, 1984.
Ibn al-Bannāʾ, 1994. Rafṯ al-ḥijāb ṯan wujūh aṯmāl al-ḥisāb, ed. by Muḥammad Aballagh. Fās: Jāmiṯat Sīdī Muḥammad ibn ṯAbd Allāh.
Ibn Ghāzī, 1983. Bughyat al-Ṭullāb wa sharḥ munyat al-ḥussāb, ed. Mohamed Souissi. Ḥalab, Syria: Jāmiṯat Ḥalab, Maṯhad al- Turāth al-ṯIlmī al-ṯArabī.
Ibn Khaldūn, 2006. al-Muqaddima, ed. ṯAbdessalam Cheddadi. 3 vols. Algiers: CNRPH.
Ibn al-KhaṬīb, 1973-77. al-IḥāṬah fī akhbār GharnāṬah. 4 vols., ed. Muḥammad ṯAbd Allāh ṯInān. al-Qāhirah : Maktabat al-Khānjī. OCLC: 32341146, 22645565
Ibn al-Qāďī, 1970-. Durrat al-ḥijāl fī ghurrat asmāʾ al-rijāl. al- Qāhirah: Dār al-Turāth.
Ibn al-Yāsamīn, 1993. Muʾallafāt Ibn al-Yāsamīn al-riyāďiyya [“Mathematical Writings of Ibn al-Yāsamīn”]. M.Sc. thesis in History of Mathematics by T. Zemouli. Algiers, E.N.S.
Lamrabet, Driss, 1994. Introduction à l’Histoire des Mathématiques Maghrébines. Rabat: Driss Lamrabet.
Lamrabet, Driss, 2008. “Notes diverses sur l'enseignement des mathématiques au Maroc sous les Almohades (542-668H/1147- 1269) et les Mérinides (668-870 H / 1269-1465)”. Pp. 19-48 in: Bennacer El Bouazzati, ed., Les Institutions de Science et d'Enseignement au Sein de la Civilisation Islamique. Rabat: Faculté des Lettres.
Loth, Otto, 1877. A catalogue of the Arabic Manuscripts in the Library of the India Office, vol. 1. London: India Office Library.
Mannouni, Mohamed, 1977. al-ṯUlūm wa’l-ādāb wa’l-funūn ṯalā ahd al-muwahhidīn [“Sciences, Letters and Arts in Almohad’s Time”]. Rabat: Dar al-Maghrib, 1977.
Marre, Aristide, 1865. “Le Talkhys d’Ibn AlBannāʾ, traduit pour la première fois (d’après un Ms. inédit de la Bibliothèque Bodléienne coté « Marsh 378 », (n.o CCXVII du Catalogue d’Uri)”. Atti dell’Accademia Pontificia de’Nuovi Lincei 17, 289-319.
Oaks, Jeffrey A. and Alkhateeb, Haitham M., 2007. “Simplifying equations in Arabic algebra”. Historia Mathematica 34, 45-61.
Oaks, Jeffrey A., 2010. “Equations and equating in Arabic mathematics”. Archives Internationales d’Histoire des Sciences 60, 265-298.
al-Qalaṣādī, 1999. Sharḥ Talkhīs aṯmāl al-ḥisāb. Oeuvre mathématique en Espagne Musulmane du XVe siècle. Edited and translated by Farès Bentaleb. Beirut: Dār al-Gharb al-Islāmī.
Riďā Kaḥḥāla, ṯUmar, 1973. Al-Muntaḥab min makhṬūṬāt al- Madīna al-Munawwara. Dimashq: Majmaṯ al-Luga al-ṯArabīyya.
Rosenfeld, Boris A. and Ekmeleddin İhsanoğlu, 2003. Mathematicians, Astronomers, and Other Scholars of Islamic Civilisation and their works (7th-19th c.). Istanbul: Research Centre for Islamic History Art and Culture (IRCICA).
Saidan, A. S., 1986. Tārīkh ṯilm al-jabr fī l-ṯālam al-ṯArabī [“History of Algebra in Medieval Islam”]. 2 vols. Kuwait: Al- Majlis al-WaṬanī lil-Thaqāfah wa’l-Funūn wa’l-Ādāb, Qism al- Turāth al-ṯArabī.
Schwartz, Randy, 2005. “Issues in the origin and development of Ḥisāb al-Khataʾayn (calculating by double false position)”. Pp 275- 296 in: Association Tunisienne des Sciences Mathématiques. Actes du huitième colloque Maghrebim sur l'histoire des mathématiques arabes: Tunis, les 18-19-20 Décembre 2004. Tunis: L'Association Tunisienne des Sciences Mathématiques.
Sesiano, Jacques, 1999. Une Introduction à l’Histoire de l’Algèbre: Résolution des Équations des Mésopotamiens à la Renaissance. Lausane: Presses Polytechniques et Universitaires Romandes.
Tashkandy, Abbas Saleh. A Descriptive Catalogue of the Historical Collection of the Scientific Manuscripts at the Library of ‘Arif Ḥikmat in Medina, Saudi Arabia. Pittsburgh: University of Pittsburgh, 1974.
al-Tunbuktī, 1989. Nayl al-ibtihāj bi-taṬrīz al-Dībāj. Ṭarābulus (Tripoli): al-Jamāhīrīyah al-ṯArabīyah al-Lībīyah al- Shaṯbīyah al- Ishtirākīyah al-ṯU?m?, al-Kullīyah, 1989.
Woepcke, Franz, 1863. “Mémoire sur la Propagation des Chiffres Indiens”. Journal Asiatique, 6th series, vol. 1, 442-529.
[1] Marre 1865; Ibn al-Bannāʾ 1969.
[2] Ibn al-Bannāʾ 1994; Aballagh & Djebbar 2001, 59, 99-104. Lamrabet 1994, 82 mistakenly attributes the date of AH 701 to the Talkhīṣ.
[3] See: al-Ghurbī L #399, al-Mawāhidī L #414, Ibn Qunfudh L #425 RI #780, Ibn Zakariyyā RI #793 [M1], al-ṯUqbānī L #428 RI #781, Ibn al-Hāʾim RI #783, Ibn Haydūr L #429, Ibn Marzūq L #435, Ibn Majdī RI #815, al-Ḥabbāk L #445 RI #831, al-Qalaṣādī L
[4] Some manuscripts show minor variations due to copy errors, such as “al-Hawāzī” for “al- Hawārī” and “Dāwūd” for “Dāwud”. Also, some historians write “al-Huwārī”. The only MS we have seen that indicates the vowel is the title page of Escorial 953/1, reproduced in [Ibn al-Bannāʾ 1969]. There it is “al-Hawārī”. The vocalization “Hawārī” (as opposed to “Huwārī”) is indicated on the title page of Madrid, Escorial MS 953/1.
[5] [Lamrabet 1994, 97-8; Ibn Khaldūn 2006 vol. 3, 460]. The Moroccan historian al- Mannouni shows the kunya instead as al-Misrātī, with an “s”, not “ص” [Mannouni 1977, 28]. This orthography is used in [Ibn al-Bannāʾ 1969] and repeated by Lamrabet, and [Aballagh & Djebbar 2001]. All the MSS show it as “ص”.
[6] from Ḥāwī al-lubāb fī sharḥ al-Talkhīṣ by Ibn Majdī (d.
[7] from al-Qawl al-mubdiṯ fī sharḥ al-muqniṯ by SibṬ al- Māridīnī (d. 1506),
[8] This is the same title of the Cairo manuscript (see below).
[9] [Ben Cheneb 1920].
[10] [Loth 1877, 225].
[11] [Ibn al-Bannāʾ 1969, 8].
[12] [Ibn al-Yāsamīn 1993, 136-144].
[13] from Kitāb al-tamḥīṣ fī sharḥ al-Talkhīṣ and 2 from
[14] Edited under the title Kitāb al-jabr wa’l-muqābala, again by Saidan [Saidan 1986, vol 2], and translated into French by Djebbar in his unpublished doctoral thesis: “Mathématiques
[15] from ten other authors.
[16] Paragraphs taken from Rafṯ al-ḥijāb but absent from Talkhīṣ how to add successive numbers starting with a number greater than 1 (p. 228.13-16 in [Ibn al-Bannāʾ 1994]),
[17] Madina MS, ff. 21b.-6, 50a.-3, 51a.-2.
[18] Madina MS fol. 8b.-3. This should be placed just after [Ibn al-Bannāʾ 1969, 42.12]. The disparity is the difference between consecutive terms. In the example given by al-Haw×rī six numbers, starting with 10, have a disparity of three. So the sequence is 10, 13, 16, 19, 22, 25. So 3 (the disparity) multiplied by 5 (the number of number less one) gives 15,
[19] [al-Qalaṣādī 1999, 52].
[20] [Ibn al-Yāsamīn 1993, 136.6-12]. See [Djebbar 2002, 221].
[21] This is paraphrased in [Ibn Ghāzī 1983, 90.14-15].
[22] Madina MS, ff. 3b-4a.
[23] The figures for these numerals are taken from the Istanbul MS.
[24] [Saidan 1986 vol 2, 510-533]. The common examples are on pp. 526-7.
[25] [Ibn al-Bannāʾ 1969, 88].
[26] [Schwartz 2005, 278, al-Qalaṣādī 1999, 233; Woepcke 1863, 510-513]
[27] The “scale” is the presumed (false) solution that is placed in the scale in the diagram. The “error of each scale” is the difference between the value calculated with the scale and the given “assigned” result.
[28] [Ibn al-Bannāʾ 1994, 297.17-18].
[29] [Ibn Ghāzī 1983, 209.16].
[30] Madina MS, ff. 53b-54a.
[31] Gregorian February 24, 1305.
[32] [Ibn al-Bannāʾ 1994, 299.3-300.22].
[33] Starting at Madina MS, fol. 54a.18.
[34] “The dome” is the place above the center of the diagram.
[35] [Saidan 1986 vol. 2, 570-1].
[36] [Saidan 1986 vol. 1, 224-8].
[37] Starting at Madina MS, fol. 55a.10.
[38] [Sesiano 1999, 79-83].
[39] [Ibn Ghāzī 1983, 218-222].
[40] See [Oaks 2010] for a study of ṯadala in Arabic mathematics.
[41] [Ibn al-Bannāʾ 1969, 73.9].
[42] [Ibn al-Bannāʾ 1994, 309.7].
[43] [al-Qalaṣādī 1999, 248].
[44] [Harbili 1997, 381.2].
[45] See [Oaks & Alkhateeb 2007, section 4.1].
[46] Madina MS, f. 59b.16.
[47] [Maestro Dardi 2001, 119.24]. We have replaced Dardi’s notation with modern notation. In other examples Dardi writes raghuaglia le parti when there is only a restoration, and also where both a restoration and confrontation are performed.
[48] MS Istanbul, Aya Sofya 4830, ff. 81a-86a. See [Djebbar 2004; Djebbar 2007].
[49] These three problems are not included in the latest book written on Ibn al-Bannāʾ’s works : [Aballagh and Djebbar 2001].
[50] [Ḥājjī 1996, vol. 2].
[51] Ibn al-Qāďī (who also versified the Talkhīṣ) names Ibn Qunfudh, al-ṯUqbānī, Ibn al- Hāʾim, Ibn Haydūr, and al-Qalaṣādī [Ibn al-Qāďī 1970], while al-Tunbuktī names Ibn Qunfudh, al-ṯUqbānī, Ibn Haydūr, al-Qalaṣādī, and Ibn Ghāzī [al-Tunbuktī 1989]. [Ḥājjī Khalīfa 2000 vol. 2, p. 400 (#3532)].
[52] I.e. Ibn al-Bannāʾs book Maqālāt fī’l-ḥisāb (“Conversations on Arithmetic”).
[53] Ibn al-Yāsamīn: Madina MS fol. 23b.12; [Ibn Ghāzī 1983, 90.2]. Ibn Ṭāhir: Madina MS fol. 51a.13; [Ibn Ghāzī 1983, 201.17].
[54] For the complete list see [Abdeljaouad 2011, 10-13].
[55] Istanbul, Süleymaniye Library MS Esad Efendi 3150/2, ff. 10b-90a, ff. 97-98, and ff. 105-110.
[56] [Ibn al-Bannāʾ 1969, 44.13-24].
[57] See footnote 53.
| Source note: Abdeljaouad, Mahdi; Oaks, Jeffrey A. «Al-Hawārī’s commentary on Ibn al-Bannā’’s Talkhīs: Contents and influences». Suhayl. International Journal for the History of the Exact and Natural Sciences in Islamic Civilisation, 2013, Vol. 12, p. 9-44, https://raco.cat/index.php/Suhayl/article/view/280204. |

