Roshdi Rashed

Islamic manuscripts have received intensive and renewed interest over the last five decades. During that period, institutes specifically concerned with manuscripts have been established, and collections of manuscripts have been organised and classified. An example is the Iranian Collection. The institutes are both public and private, such as Al-Furqān Islamic Heritage Foundation, which is hosting our meeting today. Yet despite these commendable and important endeavours, the condition of Islamic manuscripts remains bewildering to students and observers alike.
Although the Islamic tradition has the richest and largest manuscript heritage which has been preserved, it has been the least studied, edited or even indexed. This contradiction still prevails in the field of Islamic manuscripts. The road is still long and the trail is rugged. My purpose here, however, is not to investigate the reasons for this contradiction and its continuation. I have only mentioned this state of affairs at the outset to draw attention to the fact that such a contradiction becomes more serious when we look in particular at the tradition of scientific and mathematical manuscripts.
Scientific tradition has not enjoyed the same good fortune as have the traditions of religion and literature. Religious institutes. and educational centres have trained and graduated scholars who took care of the tradition in their field of interest, pacing due attention to it and bringing some of it to light. Scientific tradition has not been so fortunate.
There are other reasons to speak in particular about Arab scientific manuscripts. I shall mention a few of these here. When we look at the manuscript of mathematics and science produced by Islamic civilisation we see that they include contributions from ancient civilisations, as well as innovative research. The literature contains both what has reached us from ancient civilisations including the Greek, the Indian, the Persian , and the Syriac, and discoveries made from the beginning of the second century AH.
This is the first characteristic of the tradition of mathematical, scientific, and philosophical texts that distinguishes it from those of religion and literature. Muslim scholars were aware of this difference when they distinguished between ancient and modern science.
The second characteristic of scientific tradition was its unified language. Scientific works were written mainly in Arabic. This was the case not only in Arabic-speaking countries but also in countries where different languages were spoken. Arabic was the language of science from Samarkand to Granada including places as far apart as Khurasan and Sicily. When a scientist became nostalgic and wrote in his mother tongue, particularly Persian, as did al-Nasawī and Naṣīr al-Dīn al-Ṭūsī, he would soon re-write his work in Arabic. This was what al-Bīrūnī meant by stressing that Arabic was the language of science in his time
It is no exaggeration to say that with the beginning of the third century AH there was a language of science, and that this language was Arabic. Arabic in turn acquired a universal dimension. It was no longer a language of a single people or of a single nation, but the language of different peoples and various nations. It was no longer the language of a specific culture but of rational knowledge, whether scientific or philosophical.
The third characteristic of the scientific manuscript tradition is closely connected to the universality of the science that evolved and developed within the Islamic civilisation. The fact that science was written in only one language meant that for the first time in history science was universal in its development and its availability. We cannot gain knowledge of texts of the scientific tradition without knowing what has been translated of this tradition into Latin, Hebrew, Greek Byzantine, Italian and other languages.
This short overview shows us the historical, technical and linguistic difficulties that faced those wanting to study and edit scientific manuscripts. Talking about difficulties can be protracted and diversified, eventually leading us to the question of the relationship between the textual tradition and the conceptual tradition, and the method required for understanding them both and their relationship to each other. In many cases we discover a text when we attempt to write the history of scientific thought. Often we ntay not be able to write the history of scientific thought without a thorough knowledge of the history of the text. This close link between the textual and the conceptual traditions stood in the way of the editing of many scientific manuscripts. To solve this problem, at least in part, we first have to study the textual tradition.
Scholars endeavouring to edit and study scientific texts have been faced with various types of textual tradition. I shall first list these types of texts, then discuss them very briefly They are:

- The absent text
- The hidden text
- The truncated text
- The summarised or abridged text
- The complete text in a unique manuscript
- The complete text in multiple manuscripts
- The master copy or the author's manuscript
In all these types of manuscript, with the exception of the last, we have to differentiate between a text translated from Greek or another language, and one written in Arabic. We also have to consider which is the most effective way of approximating the original text and its authenticity if this is at all possible.
The absent text
It may seem unusual to star tour discussion of scientific manuscripts considering those which are, despite investigation, still virtually lost or at least yet to be discovered. However, we cannot avoid it: we have lost so many that are vita1 to the understanding and recording of the history or the scientific tradition. For example, the Arabic translation of Ptolemy's Optica has been lost, and all we are left with is the Latin translation of the Arabic text. We have lost too the book of arithntfic by al-Khwārizmī; all that remains is a muddled Latin translation. Also, al-Kindi's book on De Causis Diversitatum Aspectus is lost, and we only have the Latin translation.
Obviously we cannot overlook these books if we want to understand the achievements made in astronomy, mathematics and optics since the beginning of the third century AH, whether in the East or in the West. In this respect, we are fortunate to have Latin translations of some of the texts. The sad fact remains, however, that so many important books have been lost. Naturally our discussion will have to be restricted to those texts whose trails are able to follow in one way or another and that we have knowledge of. Our discussion will therefore be restricted to certain types of texts while others will be ignored.
(a) The first type of absent text is one of which we have an edition, commentary or translation in another language. An example of this type is Banū Mūsā's treatise in the third century AH on the measurement of plane and spherical figures. The treatise has rightly been considered as one of the most important books to be written in the field of analytical mathematics since the time of Archimedes, almost one thousand years earlier. In this book, Banū Mūsā presented in Arabic an extensive piece of research in that branch of mathematics which has been the basis for teaching and research both in the East and in the West. There is evidence that the book was in circulation amongst mathematicians until the sixth century AH. It then disappeared completely, immediately after Naṣīr al-Dīn al-Ṭūsī had produced an edition of it. How did this happen?
A new form of literary writing that was known as the ‘‘edition’’ of scientific and literary texts appeared in the sixth century AH, for reasons that I do not intend to go into. This form of writing reached its peak in mathematics in the works of Naṣīr al-Dīn al-Ṭūsī, Ibn Abi Jarada and others. Among these was an edition made by Naṣīr al-Dīn al-Ṭūsī of Banū Mūsā's book, which was added to collections entitled "The Intermediaries". These books were intended for training students in the study of astronomy.
Thus, the edition of Banū Mūsā's book by al-Ṭūsī became a widely circulated textbook, with many copies. This edition with other books from The Intermediaries, remained one of the books taught in schools and educational centres.
The widespread availability of this edition led to neglect of the original. Banū Mūsā's book fell into oblivion and was rejected by copyists. Those researching the manuscript tradition will be faced with the following problem: from the legitimacy point of view they should have seen the original to be able to examine the edition. The edition can only be evaluated in comparison with the original work when its veracity can be judged. In reality, however, we have to start from the edition to get to the original. The matter here goes much further the tradition of texts because of the important role played by Banū Mūsā's text in the history of that branch of mathematics. It has inspired and been studied by master mathematicians such as Thābit ibn Qurra, al-Māhānī and Ibn al-Haytham.
How then can we approach an absent text in these circumstances? This should be the aim of the researcher who wants to edit a manuscript tradition. The editor does not have many options. First of all he should establish exactly what Naṣīr al-Dīn al-Ṭūsī himself meant by edition, and what his method was. Was an edition in the sixth century AH an interpretation of the original text, rewriting it using its very words or was it producing a summary of it, or was it something else? When we can establish what al-Ṭūsī meant by an edition we will be able to assume what he would have included in or omitted from the text.Naṣīr al-Dīn al-Ṭūsī did not take the trouble to answer this question, and no one else took it upon himself to do so, despite the importance of the matter to all those engaged in the study of the manuscript tradition.
Obviously, in these circumstances we have no option but to start researching the manuscript tradition of Naṣīr al-Dīn al-Ṭūsī's text in order to determine the relationship of his edition to the original text. Here we will be faced with many difficulties. The first of these will be the need to list and enumerate edition manuscripts. In fact, the available indices of Islamic manuscripts are nothing more than lists of their titles. Moreover, these are far from being comprehensive However, assuming that such listing is at all possible, we will not be able to obtain copies of manuscripts, particularly of those kept in Muslim countries.
It is only with a great deal of effort that we have been able to obtain twenty-five manuscripts of al-Ṭūsī's editions. These are sufficient to enable us to write the history of the textual tradition of al-Ṭūsī's editions and to draw the family tree of manuscript tradition. To do this we have followed a method that has been established for three decades. The method was inspired by developments made after examination of Latin and Greek: texts, in addition to what we have acquired from the disciplines developed in Islam to study the Hādith (the narrative related to the deeds and utterances of the Prophet Muḥammad) and the science of testimony criticism, in order to take into consideration specific characteristics of the Arabic and Islamic tradition. This could be the subject of another lecture; I shall not go into it now.
The study of the history of manuscripts cannot be undertaken without also learning about the conceptual tradition, that is, Archimedian mathematical concepts and their development in the third century AH, in order to determine what is sound, what is good, what is weak and what should be excluded from the manuscript tradition. The study is summarised in the following family tree:
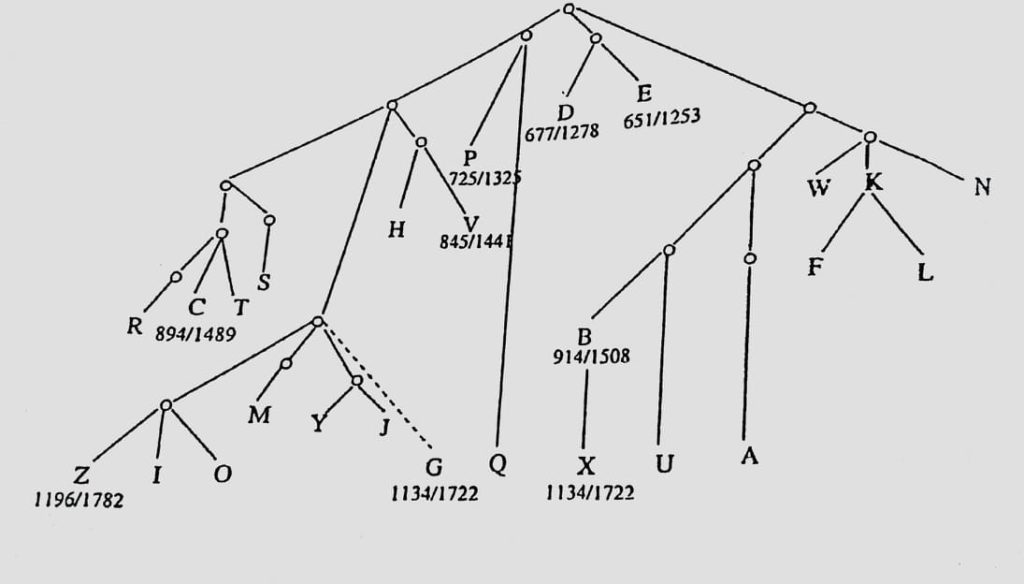
This was an initial step, which assured us of the authenticity of al-Ṭūsī's edition and provided a point of departure for our endeavour. Nevertheless, it did not bring us any closer to the absent text. We needed to find other traces of Banū Mūsā's work or, in other words, other witnesses who had actually seen the original book. After two decades of investigation our efforts have been rewarded. We have discovered two propositions from Banū Mūsā's work quoted by an unknown author in the sixth century AH. These were in a unique manuscript which was part of the Hyderabad Manuscripts in India and had not been studied before. We can now compare part of the original text with al-Ṭūsī's edition.
We can draw two conclusions from that comparison. The first conclusion concerns the relationship of the edition to the original work, and the second concerns the general issue of that literary form of writing which flourished in the 6th century AH, that is, the edition of scientific works. Some people might question. The results of that comparison and might even reject it altogether on the grounds that it was based on only two propositions Assuming that their objection is valid (and I do not think it is) we have then to refer to the Latin version of Banū Mūsā's book on which research and teaching in medieval Europe were based.
There are two Latin translations of Banū Mūsā's book - a poor translation by Plato of Tivoli and an accurate one by Gerard of Cremona. However, Gerard did miss out a proposition on mechanical or ingenious devices which was probably too difficult for him to understand. So now it is possible to compare the translation of Gerard with, on the one hand, the edition of al-Ṭūsī and, on the other, the two propositions of the Hyderabad manuscript.
This comparison demonstrates quite clearly that the translation by Gerard of Cremona was word for word and also that al-Ṭūsī's edition did not deviate from the structure of the original work or change the structure of the author’s mathematical proof inn the slightest, nor did he add his own words to those of Banū Mūsā. All al-Ṭūsī did was to summarise the work by leaving out introductory paragraphs in which Banū Mūsā explained his aims. He also left out repetitions and phrases that did not seem to add to the meaning or to be necessary for the proof. The aim of the edition was to present an eloquent and summarised text for teaching purposes. Al-Ṭūsī's method was to recompose long sentences by using connecting articles and omitting common phrases for formulating a proof, such as: ''I say, for example, quod erat demonstrandum (which was to be demonstrated)'' and. Similar phrases. He was true to the meaning of the text, keeping to its ways of expression without being restrained by them.
Figure 22

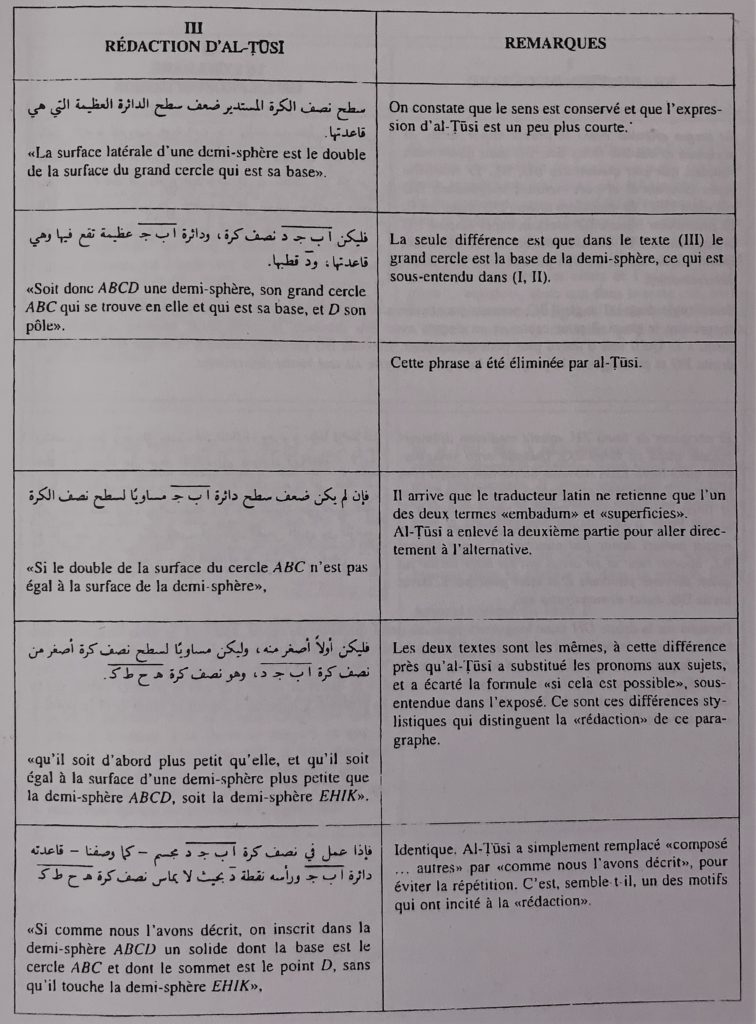


As a result of these comparisons we were able to deduce the absent text. We could get an idea of without actually laying our hands on it. We could talk about it and learn about its influence. This was actually our objective. We can even retranslate the Latin version into Arabic now that we are familiar with the vocabulary, expressions and mathematical style of Banū Mūsā.
(b) The second type of absent text is one which we have only in part in an edition or in a translation. For the sake of consistency we will stay with Banū Mūsā and also particularly with al-Ḥasan ibn Mūsā who had been widely acclaimed as a mathematical genius.
Al-Ḥasan ibn Mūsā wrote a book on the ellipse of the sun that became one of the most important works in mathematics to be written in the third century AH. In this book he explored a hitherto untried method of researching conic sections that led him to discover a whole new field, a field that his successes did not hesitate to explore further. It was the field of affine transformations.
Thābit ibn Qurra, a disciple of al-Ḥasan ibn Mūsā, was inspired by this book and talked about it with due reverence. The book also inspired Ibrāhīm ibn Sinān, a grandson of Thābit ibn Qurra, and it was mentioned by Aḥmad ibn Muḥammad ibn ‘Abd al-Jalīl al-Sijzī in the late 4th century AH. However, we know no more about this book other than its title. Its disappearance made it impossible to write the history of conic sections, a topic that was at the forefront of mathematical research
A breakthrough came only when we discovered a Hebrew translation of the work of Abū al-Qāsim Aṣbagh ibn al-Samḥ, an Andalusīan mathematician who was born in Cordoba, lived in Granada and died in 426 AH. He quoted part of al-Ḥasan ibn Mūsā's book in his own book, The Grand Book of Geometry, which is one of the many that have been lost. Qalonymos. Ibn Qalonymos in the early 14th century AD rescued part of Ibn al-Samḥ's book by translating it into Hebrew under the title A Treatise on Cylinders and Conic Sections, which included 21 propositions. Fortunately, the translated part contained what lbn al-Samḥ had copied from al-Ḥasan ibn Mūsā. The question now is, how can we discover the text of al-Ḥasan ibn Mūsā through the Hebrew version of a text written by Ibn al-Samḥ? We are faced with many intermediaries and many languages, making it very complicated.
In such cases, the role of the conceptual tradition in researching the textual tradition becomes more important. Our method was to start by investigating the history of conic sections in the middle of the third century AH, that is, before Hilāl ibn Hilāl al-Ḥimsī completed the translation of the first four books of the Treatise on Conic Sections by Apollonius. We then investigated what Thābit ibn Qurra, a disciple of al-Ḥasan ibn Mūsā, said on the subject, in order to determine what he had quoted from al-Ḥasan ibn Mūsā. We followed this by a linguistic investigation into the original Arabic words for which we have the Hebrew equivalent, particularly since the terminology of conic sections was formalised a later stage after Apollonius's work had been translated. To sum up, we had to restructure the book in order to distinguish between the authentic and the foreign. We also had to scrutinise the language of the text in order to determine what had remained the language of the third century AH and what had been introduced at a later period.
Figure 33
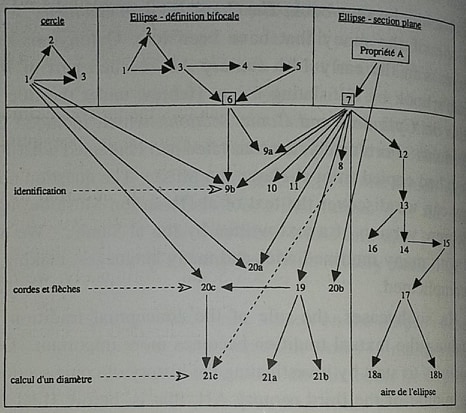
- Les propositions 2 et 3 relatives au cercle ne sont pas utilisées
- 20 est une autre démonstration de 8
There are other categories of absent texts, apart from those we have already mentioned, which are no less relevant to the research into the textual tradition. I say this only to remind you of their existence: to discuss them would take more time than we are permitted here. Among these categories are absent texts of which only a complementary work-by a later author has reached us. An example of this category is a book written Abū al-Alā ̓ ibn Sahl in the 4th century AH in which he dealt with certain mathematical problems, analysing them geometrically without going back to write the synthesis4. At a later stage al-Shannī wrote the synthesis of the problems which Ibn Sahl had analysed. Ibn Sahl's book has been lost, but we have al-Shanm's article which has paved the way to understanding the analytical method used by Ibn Sahl and to reconstituting the contents of his book, even though the words are not his.
There are also texts whose authors themselves admitted had been lost. An example is Ibn Sinān's work on the measurement of parabola. He revised and corrected his original work, and then wrote another treatise on the subject, drawing attention to the loss of the first5. The discovery of the first treatise would be of importance to those who wanted to follow up the development of the mathematical thinking of Ibn Sinān. Fortunately, we have recently found the treatise lost by Ibn Sinān in the middle of the 4th century AH and it has helped us understand the criteria for editing mathematical texts in that period.
Following this brief review we may now move on to deal with a different type of text, the hidden text.
The hidden text
One text may hide another, either intentionally or accidentally. The hidden text twill not then be ascribed to its actual author but to the author of the text obscuring it. In such instances, there would be a great deal of confusion and guesswork either in the area of the textual tradition or the conceptual tradition and in the history of both. There are many cases of the unintentional hiding of texts; sometimes it was caused by errors made by copyists and bookbinders, but there were also other reasons.
Some cases of the intentional hiding of texts have been due to plagiarism. There were also other commercial reasons. This will be a protracted and difficult subject, the discussion of which has not yet begun. I shall mention a single example to show how serious the matter is.
Aḥmad ibn ʻĪsā, in the tenth century AD, wrote a book on optics entitled Optics and Burning Minors. This book has been copied several times, including once in Hebrew characters. When reading it we should remember that its linguistic sife is very old. This was the conclusion reached W the German scholar Krause, who was one of the compilers of the indexes of Istanbul Manuscripts. He therefore thought that the book belonged to the middle of the third century AH. Most historians who have examined the book without due care have agreed with Krause.
This was the situation before we discovered several texts written by Abū Isḥāq al-Kindī which had been included in Ibn ʻĪsā's book. The problem came to a head when we recently discovered a lengthy book by al-Kindī which had been unknown for several centuries, entitled Rectification of Errors and Difficulties due to Euclid’s Optics. In this book al-Kindī put forward for the first in history a critical explanation of Euclid’s optics.
Comparing Ibn ʻĪsā's book with that of al-Kindīmade us realise without the slightest doubt that Ibn ʻĪsā had copied at least one fifth of al-Kindi's work without mentioning the latter's name, saying only: "... philosophers and Euclid among them..."6
Close examination indicated that Ibn ʻĪsā's book also included other texts taken from al-Kindi's works, particularly important parts of his book De Causis Diversitatum Aspectus, which was the first book on the subject in Arabic and has not yet been found. Only the Latin translation has survived. In this way Ibn ʻĪsā's book concealed many works by al-Kindī and kept them hidden for more than one thousand years.
We know how much Arab critics of the past were concerned about plagiarism, particularly in the field of poetry. Research into the problem of plagiarism has played an important role in the development of criticism of poetical and literary texts. Obviously we now have a duty to investigate the plagiarism of scientific texts in order to develop a method of researching the tradition of scientific manuscripts. We have actually started to research this subject in our critical editing of books on optics written in the third century AH, either translated from Greek or written in Arabic, and to pursue the appropriate method with the aim of uncovering hidden texts.
The truncated text
In the textual tradition many books have come down to us incomplete. Paragraphs or sheets and, in some cases, parts of or complete chapters are missing. Often these omissions occurred during the process of copying. There could be various reasons for this which we will not enter into here. This was the case in al-Kindi's book On Rays, Ibn Sahl's treatise On Burning Instruments and al-Qūhī's book On the Art of the Astrolabe by Demonstration. These are some of the most important works written in their respective fields. Al-Kindi's book was the first in Arabic on burning mirrors7, and in i the built on the work of his predecessors such as Anthemius of Tralles, revising his theories and adding his own contributions. Ibn Sahl's book8 was the first in the history of optics in which a geometrical theory of optical lenses and Snell's law of refraction were formulated. Al-Qūhī's book9 was also the first in the history of mathematics to study geometrical projection as a branch of mathematics. These are only a few examples, to which we may add many other books of the first order written by Ibn al-Haytham in astronomy and Ibrāhīm ibn Sinān on shadow instruments. Clearly these truncated texts represented the core and substance of all Arabic mathematical writings, so those who aim to study scientific manuscript tradition must study them well.
These texts can be classified according to the type of truncation and the possibility of restoration.
The first type of truncation is where part or parts of the text itself have been severed. An example is al-Kindi's book On Rays in which he expounded for the first time in Arabic his theory on burning mirrors. It is worth noting that the book was the beginning of a movement to research catoptrics- Only one copy of this text was known in Patna, India which had been copied in Cairo in 890 AH. The manuscript was torn in many places and difficult to understand. It was therefore not greeted with the interest it deserved, and it became a target for unjustifible criticism until we edited it with other manuscripts by al-Kindī on optics. It then be gone clear that the first part omitted from the manuscript was from the seventh line onwards (photo 4-1, 4-2). The copyist realised that this part was missing and left the rest of the page blank. The second part omitted was between proposition no 15 and the last proposition, no. 16. In this instance too the copyist noticed there was a part missing and left a gap (photo of the manuscript 5-1 and photo of the editing 5-2)- The missing part covered the end of one proposition and the beginning of the next, and misled researchers into thinking that the two propositions were one.
Photo-4.110

Photo 4-211

Photo 5-1 12

Photo 5-213

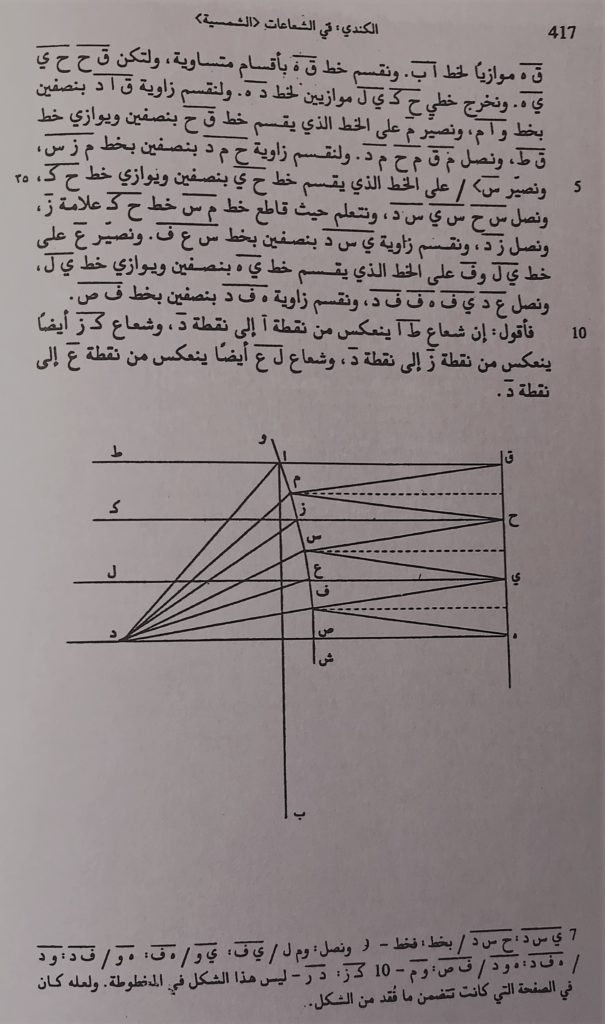
Before editing al-Kindi's manuscript we were fortunate to discover the Arabic translation of the text of Anthemius of Tralles. This helped us to fill a large part of the first gap. We suggested in the course of our study of the conceptual tradition of optics that a paragraph should be written to fill the second gap.
It was only two months after the publication of our book on the works of al-Kindī in optics that we learned by coincidence of the existence of another manuscript, of the same text, on rays. It was part of a private collection whose owner was kind enough to send me a photocopy of the manuscript in colour and on glossy paper. This is the oldest Arabic scientific manuscript. It was copied in Shawwāl in 290 AH, approximately three decades after al-Kindī died. At the end of the manuscript there is written, in different handwriting, the following," a copy of which was made in my handwriting in Dhū al-Qaʻda in 890 AH, having prayed to God to give its owner a long life, written by ʻUmar ‘Abd al-‘Aziz al- Fayyūmī" . We realised then that the manuscript we were researching must have been copied that manuscript.
On comparison it is apparent that the latter must have been copied from the former. The reason for taking out the missing part became clear: a page had been lost from the first part of the book. We were able to restore a large pan of it and also another page which was lost just before the end of the book. It became obvious that the loss of the two sheets from the old manuscript happened before 890 AH.
This example shows in an experimental way; if we can use this expression, the close connection between the textual tradition and the conceptual tradition in our attempt restore a text as closely as possible to its original form.
The, second type of truncation of texts may happen as a result of pulling sheets off the manuscript without paying attention to the consistency of the text. This could be done intentionally for various reasons. For example, the book on burning instruments by Abū al-‘Alā’ ibn Sahl, a scientist of the 4th century AH, is considered, as I have already mentioned, to be one of the most important works written in Arabic on optics and particularly on the theory of refraction. It is impossible to understand what Ibn al-Haytham achieved without first knowing what Ibn Sahl did in that field.
We have only one manuscript of Ibn Sahl's treatise, in the handwriting of Aḥmad ibn Jaʻfar al-Ghundijānī and provided with. vowel points by ‘Alī ibn Yaḥyā al-Maghribī, the son of the well-known astronomer. The manuscript consisted of twenty-six sheets. It reached us in a disordered and truncated way- We first had to rearrange the sheets, to be able to discover the theoretical structure of Ibn Sahl's treatise. The sheets have been rearranged in the following way:
1 v--> [14 r-16v] --> [13r-v] --> [2r-12v] --> [17r-26v]
The first gap was between l v and 14r, the second between l6v and 13r. It became obvious that 10 sheets had been pulled off the manuscript. These sheets had not been pulled off off the manuscript. These sheets had not been pulled off haphazardly- They contained the author's discussion of ellipsoidal and parabolic mirrors. Therefore it seems that pulling them off was an intentional act by a reader fascinated by the two types of mirror. He did not realise, or perhaps notice, that these sheets also contained another mathematical question, namely the continuous drawing of these two conic sections.
Study of the conceptual tradition enabled us to know what had been pulled off, its place in the text and also its scientific contents. What remained for us to do was to go back to the textual tradition in order to authenticate what we had discovered through our examination of the conceptual tradition, and to ascertain if we were right or wrong. The study of manuscripts by using this method becomes a scientific investigation subject to experiment and verification- We had then to go back to various collections of manuscripts to search for the works of lbn Sahl and treatises dealing with burning minors. We were lucky enough to find another text from a philosophical collection in the Ẓāhiriyya Damascus Collections that enabled us to fill the first gap. We established that the Damascus manuscript was part of Ibn Sahl's book in the handwriting or Ibn al-Murakhkham, a Baghdad judge of the 6th century AH.
The. Third type of truncated text may be traced back to an incident which happened during the time of copying and was afterwards forgotten. An example of this type is a book Abū Sahl al-Qūhī on The Art of the Astrolabe by Demonstration which we have already mentioned and which is considered to be one of the first books to research geometrical projections as such. We know of only one manuscript of this book which is at the University of Leiden. Many chapters of the second part of the book were lost, and a large part of proposition 6 of the second chapter of the second part was also missing. The book belonged to a mathematical collection of the most important scientific collection, although it was copied at a later period.
The collection was copied in the seventeenth century AD in Amsterdam for a particular reason. At that time the Dutch orientalist, Golius, became interested in Arabic scientific manuscripts, as did many other European orientalists. Golius was a professor of mathematics in Holland and one of the scholars who corresponded with Descartes. He contributed very actively to the collection of Arabic scientific manuscripts and their transfer to Holland, borrowing manuscripts that he could not buy. He asked an Arab who was then living in Holland to copy them. Some people from the Orient refused to sell their manuscripts to him but agreed to lend them. Among the manuscripts shipped to Holland was the well-known Leiden Collection, which included many highly valuable scientific and mathematical manuscripts. We have established irrefutable evidence that the original manuscript, which was returned to its owners in Syria, is now at Columbia University as part of the Smith Collection. The collection included al-Qūhī's book which disappeared after being copied in Amsterdam. We therefore had no means of referring to the original copy in order to fill the gaps and to rectify the damage done to the manuscript when parts of it were removed.
Our method of filling gaps is based on a number of tasks. Firstly, a thorough and careful examination of the scientific or mathematical conceptual tradition must be carried out to determine which parts are missing and what they contained, in order that they can be rewritten. Secondly, the language of the existing part of the text and of other works of the author must be carefully studied to familiarise ourselves with his vocabulary. The style of the author and the way he structured his sentences and phrases is carefully scrutinised with a view to making the formulation of new phrases as close as possible to his own wording and style. Thirdly, works of the author's successors are perused to locate any quotations or comments that might help us perfect the writing of the added part, while at the same time remaining objective and cautious14
The fourth type of truncated text is the one in which parts have been lost. We have already seen an example of this in al-Qūhī's book of which many chapters of the second part were lost There are many other examples: for instance, the first three books of the Arabic translation of The Art of Algebra by Diophantus, translated by Qusṭā ibn Lūqā have been lost15 . The second and third parts of Ibrāhīm ibn Sinān's book on shadow instruments have also been lost. However, the two cases are very different. Qusṭā ibn Lūqā translated seven chapters of Diophantus' book on numerical problems and called them The Art of Algebra.
When we found this translation more than twenty-five years ago, there were only four chapters left. Fortunately , the well-known mathematician of the late tenth century AD, Abū Bakr al-Karajī, summarised the first four chapters in his book Al-Fakhī, and al-Samaw’al al-Maghribī of the filth century AH quoted some of the questions in the first three chapters. .Also, Abu Ja’far al-Khāzin referred to an important question in the third chapter. These works were of great help to us in determining the questions dealt with in the first three chapters that had been removed from Diophantus' book. The Greek text of the same chapters, which was not undistorted, was also of use to us.
Finally, by reading the works of one of the commentators of al-Karajī we were able to demonstrate beyond any doubt that the first three chapters were removed in the seventeenth century AD16. The same commentator also provided us with a number of paragraphs taken from Qusṭā ibn Lūqā's translation first three books. The Greek version, albeit with some distortion, is still in existence. We also have the commentary by al-Karajī and the quotations by al-Khāzin, al-Samaw’al and the commentator I have already mentioned. We still have the larger part of the translation, too, that is, the remaining four chapters.
These chapters give us a precise knowledge of the content of the missing part, its structure and linguistic style. We could even rewrite that part if we wanted to. In other words, thanks to the conceptual tradition and the Greek and Arabic textual tradition, it has become possible to know what is missing and to rewrite it if necessary. We have now given a number of examples of this method.
The matter is completely different as far as the second example of this type of truncated texts is concerned. Ibrāhīm ibn Sinān's treatise on shadow instruments is an example of this type: the book was written in three parts, of which the whole of the third part and most of the second part are missing. All we know about the missing parts is what was said by the author himself in his introduction to his book and what was written afterwards by Ibn al-Haytham when criticising a question in the missing part. In a case like this we do not have much hope of coming closer to the author's text because of the extreme scarcity of the textual tradition. Here we have come to a dead end, unless we are fortunate enough one day to discover another copy of a manuscript of the text or of its commentaries.
The summarised or abridged text
In some cases a copyist would interfere with the text to abridge or summarise it. In this situation we face a problem which was encountered by scholars of the Ḥadith, namely, the problem of whether it is permissible to summarise the Ḥadith, and the conditions under which this can be done while maintaining its validity For example, we learn from al-Ḥāfiẓ ibn Ḥajar in his book Sharḥ al-Nukhba that ''As regards summarising the Ḥadith, the majority of people consider it permissible, on condition that it is done by a man of learning, because he will remove from the Ḥadith only what has no relevance to what he has decided to retain. Thus, its significance will not be altered nor its eloquence distorted: the remaining text and the part omitted will be two predicates, or the stated will cover the omitted. On the other hand, a man of no learning could omit what is relevant - for example, cases of exception ".
I have quoted Ibn Ḥajar to demonstrate the importance of the matter for the scholars of the Ḥadith. Naturally, we would be expected to raise the same question when we aim to establish a new discipline to study the tradition of scientific Arabic texts. The question is whether it is permissible to consider the text valid and authoritative after it has been summarised or abridged by a copyist. For at least two reasons the matter is more difficult in the field of the tradition of scientific manuscripts than is in the field of the Ḥadith. Firstly, in the Ḥadith we have a science of testimonies criticism to differentiate between those who are authorities on the subject and those who are less so, between men of learning and others of lesser stature. Also, the abridgement as explained by Ibn Ḥajar and others had been restricted to the wording of the Ḥadith. It is different when we come to scientific manuscripts. Up till now no attention has been given to establishing a science of testimonies criticism for the study of copyist and their areas of specialisation. What makes the matter more difficult is the fact that the copyists were not all of the same class or profession as had been the case in medieval Europe. Among the copyists there are outstanding mathematicians such as al-Sijzī and Ibn al-Haytham, mathematicians of lesser calibre, such as Qādi Zādeh and Muḥammad ibn Sartāq al-Marāghī; judges, such as Ibn al-Murakhham, whom I have already mentioned; Sufis, such as al-Mawla Dāwūd al-Qayṣarī al-Qarmānī, and clerks of the diwan (government departments) with training in mathematics, such as Muṣṭafā Ṣidqī- There are also people who had no knowledge about what they were copying. For the time being, until a science of testimonies criticism for the study of copyists has been established, we have to be very careful.
The second reason for the matter being more difficult in the field of the tradition of scientific manuscripts is that mathematical and scientific texts, unlike the Ḥadith, were written in technical language, with very little attention paid to the art of good style. They contained many tables and geometrical drawings, which made summary or abridgement different and difficult. Before making a judgement in this matter we can look at an example from a book by Sharaf al-Dīn al-Ṭūsī in the fifth century AH On Equations17.
This book by al-Ṭūsī was the most important work in Arabic on algebra and algebraic geometry and the most difficult to understand. The author reviewed in his book what he had inherited from his predecessors on the theory of algebraic equations, in order to perfect and verifies it. He followed the method of his predecessors to attain its utmost potential. Al-Ṭūsī also achieved what his predecessors had not attempted: in his book he arrived at the Ruffini-Horner method of the numerical solution of algebraic equations, and he wrote a complete theory to justify his method. He formulated his theory without resorting to symbols. He also came near to the beginning of mathematical analyses and arrived at concepts and conclusions which historians have claimed were innovations of mathematicians of the seventeenth century AD.
We looked for al-Ṭūsī's book, but all we could find was a unique manuscript at the India Office in London which was copied in 1198 AH (1784 AD). The manuscript was in the handwriting of one of the Hyderabad copyists who had copied several mathematical and astronomical manuscripts. We hesitated for a long time about editing this difficult manuscript because of its late date and the possibility of its containing material that was not in its original version. After many years we finally managed to obtain the original version from which the manuscript at the India Office was copied. The original was a manuscript written in the eighth century AH: the first sheets were missing so the author had remained unknown. We also found another paragraph in a manuscript at the Library of Venice. It then became possible to edit that difficult text, which we have now done.
The text started as follows: "My aim in this book is to provide a summary of the art of algebra and muqabala, to revise what has reached me of the words of the most distinguished philosopher, Sharaf al-Dīn al-Muẓaffar ibn Muḥammad al-Ṭūsī, and to abridge his text. I have left out the tables that be drew on the calculation and solution of the problems, as they were far from being natural and they were long and tedious. I also verified the method of deducing questions by Takht (dust table) and combined the way of solving problems with proofs, calling it equations".
It would be a serious matter if what this unknown person was saying was true, particularly since we know nothing about him, not even whether he was a man of learning or not. In such a case we had to investigate the extent of his summary and determine whether this unknown author was capable of undertaking in. To answer this question we had to compare this manuscript of al-Tūsī's book with his other works, both mathematically and linguistically.
Al-Ṭūsī wrote another treatise On the Two Asymptote Lines and he dealt with the same subject in his book On Equations. Comparison of these two texts was therefore important to reveal how much was summarised: it demonstrated beyond any doubt that they contained the same mathematical propositions and even, in most cases, the same expressions and phrases. It became evident that our unknown copyist was largely following the words of Sharaf al-Dīn al-Ṭūsī, copying his mathematical propositions and their proofs. How could it be otherwise! A careful examination of the structure of al-Ṭūsī's text, the sequence of its chapters (including premises needed by al-Ṭūsī afterwards), the investigation of equations of conic sections and their performance, and the classification of equations and their solution, led us to the conclusion that our unknown copyist was not able to summarise or revise any of these topics The comparison of parts of the texts with other parts in other words, internal criticism of the text revealed clearly that all our unknown copyist did was to copy what al-Ṭūsī had written. It seems that he omitted al-Ṭūsī's introduction, in which he explained his purpose and method. We have deduced this because al-Ṭūsī's book starts straightaway with mathematical propositions, without an introduction, even though it is one of the longest works in Arabic algebra in particular and in mathematics generally. Al-Ṭūsī's tables established for the numerical solution of equations have definitely been omitted by the copyist, thus making the book impossible for researchers to understand. Al-Ṭūsī always provided numerical tables for every equation and explained how to devise tables appropriate for equations. It is very difficult to think of this book without the tables omitted by the unknown copyist.
Photo 618

Photo 719

Evidently, internal criticism of a text will have to be based on the date of the text and at the same time on the history of mathematical thinking. This is important in discovering how much has been abridged and how to avoid the dangers of abridgement, and why it is necessary in this case to reconstruct the tables and replace the omissions so as to achieve the closest approximation to the original text. The editor of a text should himself be cognisant of the vocabulary, expert in the exact meaning of the words used and able to understand sufficiently the subject matter and the purpose of the book.
The complete text in a unique manuscript
In many cases we have a principal text which was not transcribed by the author of the text but from a missing original. This raises questions about the validity of the text and its veracity: do we accept the manuscript as it is, as an authoritative source of the text, and what are the conditions we have to consider in order to challenge its validity: To appreciate the importance of the matter we have only to remember that among those-unique copy texts are the following: the texts of Thābit ibn Qurra On the Measurement of a Cylinder and Its Sections which was one of the most important works in mathematical analysis; al-Khāzin's commentary on the first chapter of Ptolemy's Almagest (he was also one of the founders of Arabic mathematical analysis); Abū Kāmil Shujāʻ ibn Aslam's book on algebra, and other books by Ibn al-Haytam, al-Khayyām and others. This means that if we challenge the most important scientific books. On the other hand, if we accept their validity without much examination and scrutiny we may be wrong. This is a matter worthy of attention and investigation which has not yet been adequately debated.
The following criteria apply in the case of unique copy manuscripts:
- The book should be listed by authors of books of al-Ṭabaqāt (bibliographers) or earlier scholars.
- There is another textual tradition such as a commentary, edition or other corroborating text.
- There is a translation or translations of the text done at a relatively early time into languages such as Persian or Latin.
- Text and the development of his thesis should be similar in style to that used by the author in his other books.
- The linguistic style of the text should be the same as that used by the author in other writings.
These criteria, and others, definitely require intensive research.
There are several types of unique copy manuscripts, for instance:
1. The text is supported by another text – that is, the indirect textual tradition. An example of this is the text by Thābit ibn Qurra, which we have already mentioned and which was edited by Ibn Abī Jarāda in the 6th century AH. When we compare the texts, it becomes clear that the manuscript is genuine.
2. The text has been translated. An example of this are the Latin and Hebrew translations of a book by Abū Kāmil Shujāʻ ibn Aslam on algebra. Both the translations represent indirect copying, proving the validity of the text and aiding its critical editing.
3.The author used part of the book in another of his works. For example, Omar al-Khayyām wrote a treatise On the Quadrant of a Circle which exists as a unique manuscript in the Collection of Tehran University20 .Al-Khayyām borrowed some parts of his own treatise and used them in his algebraic books. In this way, plagiarism of scientific texts helps us to demonstrate the authenticity of the text and prove its veracity. This happened in the case of al-Kindi's book On the Rectification of Errors and Difficulties due to Euclid's Optics, which was quoted by Ibn ʻĪsā without mentioning al-Kindi's name.
The complete text in multiple manuscripts
This is the case with many texts. Some have survived in very few manuscripts and others in scores. Editing these texts requires their classification according to their family tree, their original root, their branches and their various copies. The editing process cannot be begun without knowing this family tree and the textual tradition. Here, the editor should avoid falling into the trap, as many have done, of thinking that the age of a manuscript is proof of its validity and authenticity. There are many examples that disprove this belief, such as the manuscript by Kamāl al-Dīn al-Fārisī on amicable numbers. Even though it was copied less than a decade after the death of its author it is of worse quality than other manuscripts of a later date. Also, the manuscript of al-Khayyām's treatise on algebra, the Vatican manuscript is the most inferior of the manuscripts of that text despite its relative age: it is one of the oldest copies of the text.
Classification of the various copies of a manuscript is not to be taken lightly, particularly when these are numerous. First,we have to establish the differences between manuscripts of the same text and how they differ, listing the deficiencies of each copy. We must recognise the fact that differences and even deficiencies do not all have the same significance. Grammatical errors in writing numbers, for example, were widely common among mathematicians of the third century AH but were never a hindrance to understanding the text, nor did they constitute a deficiency. In fact, grammatical errors in general were common in scientific and mathematical texts.
The question is, what are the most important differences between manuscripts on which we can base our classification when all that we possess is criticism of the texts themselves, that is, without recourse to external factors which might not be available to us in many cases. These external factors might be the date of the transcription, the identity of the copyist, the level of his knowledge, the quality of the copy from which he transcribed, and so on.
Undoubtedly the most important differences are those which resulted from the copyist's negligence. These are unintentional discrepancies and spontaneous errors, such as leaving out one or more sentences, missing out two or more letters, or omitting two or more numerical figures of a mathematical text. If we can assess what each manuscript is lacking compared to another, then we can use the following rules for classification:
- If a manuscript is missing sentences, letters, numbers, or figures that are not missing in another manuscript, cannot consider the former to be the only original manuscript of the latter.
- Manuscripts that belong to the same family tree will all be missing the sentences, letters, forms, and figures that are missing in any one of them.
- Manuscripts which are missing sentences, letters, or figures which are also missing in manuscripts belonging to a different family tree should be considered copies of different originals, made either at the same time or consecutively.
We have followed these evident principles for the classification of manuscripts. We now have to establish tables to enumerate what some manuscripts are missing compared to others, and also the common errors and so on. It is advisable to use a computer for this work if the number of manuscripts becomes too great for conventional methods to be effective.
The master copy or the author's manuscript
This is the easiest case. The textual tradition will be edited by tracing grammatical errors, additions and other alterations that may have been introduced to the text when it was copied from the master copy, if indeed it was.
In this short review we can come to several conclusions of which we will mention only two. The first constitutes a prerequisite for all those who work with the textual tradition. They must have a strong relationship with the conceptual tradition. Until recently, text was considered to be a 'living organism', to be copied for the purpose of research and learning. Scientific thought, its development and its decline has frequently influences this 'living organism' which, in is turn, has often influenced the Content and form of scientific thought. In a nutshell, we believe that the textual tradition and the conceptual tradition are inseparable. This must be so.
The second conclusion is vital for future development if we are to accomplish what we are working towards. We must develop certain branches of knowledge vital for the study of the textual tradition. These include a science of testimonies criticism, which will study the identity, methods and standing of copyists, the history of education and its institutions in Islamic cities, and also philology and its history. These, and other branches of knowledge, will help to lay down scientific foundation necessary for research in both the textual tradition and the conceptual tradition.
| Source note: This was published in: Editing Islamic Manuscripts on Science: Proceedings of the Fourth Conference of Al-Furqān Islamic Heritage Foundation - 29th-30th November 1997 - English version, Al-Furqān Islamic Heritage Foundation, London, UK, pp. 15-57. |


